
References and digits of Pi:
-
Here are two excellent references about pi:
- The Life of Pi, by J.M. Borwein.
- Life of Pi on slides, by J.M. Borwein.
- Also: MacTutor.
- pi to 40000 decimal digits,
- pi to 20000 hex digits,
- pi to 10000 base 36 digits,
- pi to 10000 base 62 digits (using 0-9,A-Z,a-z).
The May 6, 1993 episode of The Simpsons has the character Apu boast "I can recite pi to 40,000 places. The last digit is one." See the 40000 digits above, where the 40000th one is red. (A colleague of Borwein actually supplied this information to the Simpson's program: see "Life of Pi on slides" above.)
The most interesting decimal run in pi starts in position 762 (row 7, column 7), where 9999998 occurs (six nines in a row). The number two times pi has "...399999997..." (seven nines) at the same place. Expressions giving an approximation of pi: pi from an expression.
C program giving 15000 digits of pi:
- Rabinowitz and Wagon gave an amazing algorithm to compute decimal
digits of pi, based on the series given below. The "algorithm
uses only bounded integer arithmetic and is surprisingly efficient.
Moreover, it admits extremely concise implementations. Witness,
for example, the following (deliberately obfuscated) C program
due to Dik Winter and Achim Flammenkamp ...." (See Unbounded
Spigot Algorithms for the Digits of Pi, by Jeremy Gibbons,
Math. Monthly, April 2006, pages 318-328.)
| C program to calculate 15000 digits of pi | The Formula used |
|---|---|
a[52514],b,c=52514,d,e,f=1e4,g,h;
main(){for(;b=c-=14;h=printf("%04d", e+d/f))
for(e=d%=f;g=--b*2;d/=g)d=d*b+f*(h?a[b]:f/5),a[b]=d%--g;}
|
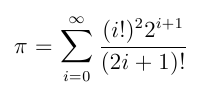
|
| Output of a run | |
| here (with newlines inserted by hand), or here |
This is called a spigot algorithm because it spits out digits as if from a spigot. Other versions of this program can be found on the Internet. Still, with this method one has to commit ahead of time to a specific number of digits to calculate. The next method doesn't have this weakness.
Calculating arbitrarily many digits of pi:
-
The Ruby release has a remarkably short and simple Ruby program that calculates
arbitrarily many decimal digits of pi. This algorithm uses
the continued fraction representation on the right below and requires
library functions that do arbitrarily large integer arithmetic.
- New How the algorithm works describes this algorithm and shows how it can be adapted to compute any continued fraction.
- Pi by continued fraction shows modifications to the Ruby program.
| Ruby program to calculate pi | The Formula used |
|---|---|
#!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 4, 1, 12, 4
loop do
p, q, k = k*k, 2*k+1, k+1
a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
d, d1 = a/b, a1/b1
while d == d1
print d
$stdout.flush
a, a1 = 10*(a%b), 10*(a1%b1)
d, d1 = a/b, a1/b1
end
end |
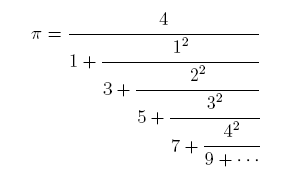
|
| Output of a run | |
% pi.rb 3141592653589793238462643383279502884 ... |
Calculating Pi using a simple series:
-
The following series (known as "Gregory's series") would seem to converge too slowly to be useful for calculating pi:
- Ordinary Slow Convergence to Pi
- Better formulas for this series
- Pi by averaging
- Pi by averaging, using an explicit formula
- The explicit formula, with N=32, A=16, T=15.
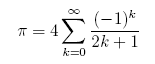
|
pi has commonly been calculated using arc tan formulas, as shown in:
Calculating Pi using another series:
-
Here is another series whose sum can be approximated just like the one above:
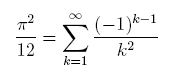
|
Everything done for Gregory's series can be done for this one: see reciprocals of squares. In particular, I discovered the following formula (without proof) that I haven't seen elsewhere:
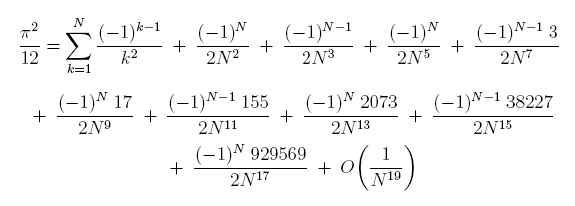
|
Here the coefficients in the numerators above (leaving off the first 1): 1, 1, 3, 17, 155, 2073, 38227, 929569, ... are called Genocchi numbers (after an Italian mathematician).
Calculating Pi using the Arithmetic-Geometric mean:
-
An advanced iterative method to efficiently calculate Pi is given at:
The algorithm gives slightly more than double the number of digits
with each iteration.
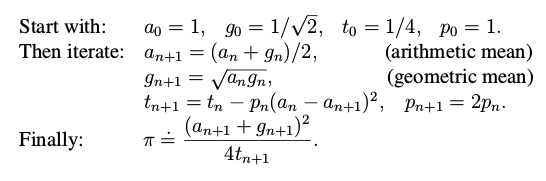
|

|
# Here is the actual run: # Prec: 70 , iters: 4 # 3.141592653589793238462643383279502884197114678283648921556617106976027 # # pi: 3.141592653589793238462643383279502884197169399375105820974944592307816 # 1 2 3 4 5 6 7 # 1234567890123456789012345678901234567890123456789012345678901234567890Here is a summary of results of the first 13 iterations, which gives more than 40,000 digits of Pi. Even though 40,000-digit floating point accuracy is required in the calculations, only relatively few operation (a hundred or so) are needed. This method is far faster than others in this writeup. The 40,000 digits of Pie are obtained on my ancient PC with no noticable delay.
# summary results for successive values of N # col 1: the value of N in the program # col 2: actual num of correct digits produced each time # col 3: = 2 times col2: expected correct digits next time # col 4: extra correct digits actually produced next time # (very slightly more than doubling each time) # 1 2 4 3 # 2 7 14 4 # 3 18 36 4 # 4 40 80 3 (this is the actual run above) # 5 83 166 4 # 6 170 340 4 # 7 344 688 5 # 8 693 1386 5 # 9 1391 2782 5 # 10 2787 5574 7 # 11 5581 11162 8 # 12 11170 22340 7 # 13 22347 > 40000 A BIT QUICKER THAN DOUBLING
Revision date: 2023-11-03. (Use ISO 8601, an International Standard.)