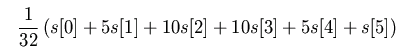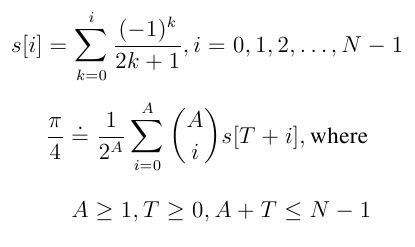
These formulas are particularly simple. The first is just partial sums of Gregory's series, while the second is a fairly simple result of the averaging. (An argument showing where the second formula comes from is given at the end of this page.) These formulas will produce 16 digits of accuracy with about 130 floating point operations. In general, the formulas can be implemented in time O(N) and in small constant space.
Here N is the number of partial sums to be stored in the array elements s[0], s[1], ..., s[N-1]. Then T is the index where the averaging starts, and A is the number of times to average, so that there are A+1 terms involved in the averaging, namely s[T], s[T+1], ..., s[T+A]. When the averaging is done, there is just one term left.
The value of N must be at least as big as T+A+1. Given A and T, there is no reason to choose a larger value for N.
Instead of repeatedly averaging with loops in a program, the averages can be calculated, giving a formula with binomial coefficients (the formula above). In what follows, we will usually be choosing an even integer for N and then taking A = N/2 and T = N/2 - 1. For fixed N, roughly these values give the most digits of Pi.
The earlier averaging program clearly implements an O(N2) algorithm, assuming that N, A, and T are of the same order: Each step takes O(N) time and there are O(N) steps.
The first formula above is O(N), but the second formula looks like it could be O(N2). It would be of this order is each binomial coeffient were calculated from scratch, but with just one multiplication and one division, we can convert each coefficient to the next one. Thus the formula can be implemented in O(N) time.
In fact, with even N, and A = N/2, T = N/2 - 1, the formula can be implemented with about 4*N = 8*A high-precision floating point operations, along with integer operations.
We will see below that for N = 32, A = 16, and T = 15, we get 16 significant digits of Pi, using about 130 operations on doubles. A later calculation, using Java BigDecimal for high precision, shows that for N up to 98, the number of significant digits of Pi obtained is roughly equal to N/2. Below, when N = 98, the computation yields about 47 digits of Pi, using about 400 of the high precision operations. (The actual code below was not structured to minimize BigDecimal operations.)
The first program below implements the formula using double precision. The program uses the transcendental function pow to calculate 2A, but this could just be a shift in binary machines. The program also uses the array s that occurs in the formula at the top, but the array is not needed; the partial sums can be calculated on the fly. Notice that no additional accuracy comes from values of N larger than 32.
| Pi by averaging, using an explicit formula | main function, and Output of a run |
|---|---|
// PiAve: Averaging using explcit formula
import java.text.DecimalFormat;
public class PiAve {
private DecimalFormat d16 = new
DecimalFormat("0.0000000000000000");
private DecimalFormat d10 = new
DecimalFormat("0.0000000");
private String diff(double r) {
double t = (Math.PI) - r;
if (t < 0) return d16.format(t);
else return " " + d16.format(t);
}
public double Ave(int N, // # terms in series
int A, // # of times to average
int T) { // starting term for averaging
// First calculate terms of
// sum(i=0; i < N; i++) + or - 1/(2i+1)
double sum = 0.0; // cumulative sum
double term2; // each term, no sign
int sign = 1; // sign of each term
double[] s = new double[N]; // succ. sums
// calc N terms of inaccurate series for pi
for (int k = 0; k < N; k++) {
term2 = 1.0/(2.0*k + 1.0);
sum = sum + sign*term2;
sign = -sign;
s[k] = sum;
}
// compute average explicitly
int term = 1; // cycles thru binomial coef
sum = s[T]; // sum = s[0];
int n = A;
int k = 1;
for (int i = T+1; i <= T+A; i++) {
term = term*n/k;
sum = sum + term*s[i];
n--; k++; // on to next binomial coef.
}
// pi approx is sum*4/2^A
double pi_approx = sum*4.0/Math.pow(2,A);
return pi_approx;
}
| public static void main(String[] args) {
int N; // # of terms in initial series
int A ; // # of times to average
int T; // starting term for averaging
// must have T+A <= N-1
PiAve piAve = new PiAve();
System.out.print (" N A T Sum");
System.out.println(" Diff");
for (int i = 1; i <= 20; i++) {
A = i;
N = A*2;
T = A - 1;
double ave = piAve.Ave(N, A, T);
if (N < 10) System.out.print(" ");
System.out.print(" " + N + " ");
if (A < 10) System.out.print(" ");
System.out.print(A + " ");
if (T < 10) System.out.print(" ");
System.out.print(T + " ");
System.out.print(piAve.d16.format(ave) +
" ");
System.out.println(piAve.diff(ave));
}
}
}
% java PiCalc
N A T Sum Diff
2 1 0 3.3333333333333335 -0.1917406797435404
4 2 1 3.1238095238095243 0.0177831297802689
6 3 2 3.1434343434343437 -0.0018416898445506
8 4 3 3.1413919413919420 0.0002007121978509
10 5 4 3.1416151787668820 -0.0000225251770889
12 6 5 3.1415900771130287 0.0000025764767644
14 7 6 3.1415929522484927 -0.0000002986586995
16 8 7 3.1415926186270062 0.0000000349627869
18 9 8 3.1415926577139115 -0.0000000041241184
20 10 9 3.1415926531003904 0.0000000004894027
22 11 10 3.1415926536481558 -0.0000000000583626
24 12 11 3.1415926535828067 0.0000000000069864
26 13 12 3.1415926535906340 -0.0000000000008411
28 14 13 3.1415926535896936 0.0000000000000995
30 15 14 3.1415926535898073 -0.0000000000000142
32 16 15 3.1415926535897927 0.0000000000000004
34 17 16 3.1415926535897944 -0.0000000000000013
36 18 17 3.1415926535897950 -0.0000000000000018
38 19 18 3.1415926535897944 -0.0000000000000013
40 20 19 3.1415926535897940 -0.0000000000000009
|
Next I have implemented the same calculation using the java BigDecimal class. The calculation below is inefficient, since Gregory's series is calculated from scratch for each new value of N, and there are other inefficiencies (such as using pow again). This makes no noticeable difference for these sizes of N.
| Same Algorithm using Java BigDecimal class | Output of a run |
|---|---|
// PiAve: Averaging using explcit formula
import java.math.*;
public class BigDTest {
public BigDecimal ave(int N, int A, int T) {
BigDecimal one = new BigDecimal(1);
BigDecimal mOne = new BigDecimal(-1);
BigDecimal[] s = new BigDecimal[N];
s[0] = new BigDecimal(1);
for (int i = 1; i < N; i++) {
BigDecimal term2 = new BigDecimal(1);
BigDecimal iVal = new BigDecimal(2*i+1);
term2 = term2.divide(iVal, 50,
RoundingMode.HALF_EVEN);
if ((i % 2) == 1) term2 = term2.negate();
s[i] = new BigDecimal(1);
s[i] = s[i-1].add(term2);
}
// compute average explicitely
BigDecimal term = new BigDecimal(1);
BigDecimal sum = new BigDecimal(1);
sum = s[T];
BigDecimal n = new BigDecimal(A);
BigDecimal k = new BigDecimal(1);
for (int i = T+1; i <= T+A; i++) {
term = term.multiply(n);
term = term.divide(k);
BigDecimal coef = new BigDecimal(1);
coef = term;
coef = coef.multiply(s[i]);
sum = sum.add(coef);
n = n.add(mOne);
k = k.add(one);
}
BigDecimal two = new BigDecimal(2);
BigDecimal scale = two.pow(A-2);
return sum.divide(scale);
}
public static void main (String[] args) {
int N; // # of terms in initial series
int A ; // # of times to average
int T; // starting term for averaging
System.out.print(" ");
for (int i = 0; i < 5; i++)
System.out.print("1234567890");
System.out.println();
BigDTest bigDTest = new BigDTest();
for (int i = 2; i < 50; i++) {
A = i;
N = A*2;
T = A - 1;
if (N < 10) System.out.print(" ");
System.out.print(N + " ");
if (A < 10) System.out.print(" ");
System.out.print(A + " ");
if (T < 10) System.out.print(" ");
System.out.print(T + " ");
BigDecimal result = bigDTest.ave(N, A, T);
System.out.println(result);
}
}
} | % java PiCalc
11111111112222222222333333333344444444445
N A T 12345678901234567890123456789012345678901234567890
4 2 1 3.12380952380952380952380952380952380952380952380954
6 3 2 3.14343434343434343434343434343434343434343434343436
8 4 3 3.14139194139194139194139194139194139194139194139196
10 5 4 3.14161517876688155325926223759041096502396811994338
12 6 5 3.14159007711302771203161565256059804451243406688287
14 7 6 3.14159295224849135200461085506179058474118374508739
16 8 7 3.14159261862700465979471637932729967357814724453988
18 9 8 3.14159265771390998101521797029481118126898103183807
20 10 9 3.14159265310038869628794031418445766749493643661662
22 11 10 3.14159265364815481015761430067669322413576871163882
24 12 11 3.14159265358280538638182580784192940988251328234157
26 13 12 3.14159265359063277623400925614927714097782568551931
28 14 13 3.14159265358969208058783230077697220214244196906960
30 15 14 3.14159265358980545785400201131451965422481241065324
32 16 15 3.14159265358979175918248057210660873357438434942285
34 17 16 3.14159265358979341788971010384522618594227085411896
36 18 17 3.14159265358979321666210279845116922581646800646284
38 19 18 3.14159265358979324111546918614545150293225498162545
40 20 19 3.14159265358979323813938863684827982259771553398277
42 21 20 3.14159265358979323850208167924066197346400996304688
44 22 21 3.14159265358979323845782635976049518490053711388007
46 23 22 3.14159265358979323846323234043973140776039749452994
48 24 23 3.14159265358979323846257130650417288581973049273458
50 25 24 3.14159265358979323846265221165227068443861473150739
52 26 25 3.14159265358979323846264230107214306926774530313716
54 27 26 3.14159265358979323846264351603696160813813491554368
56 28 27 3.14159265358979323846264336698268042173361757778101
58 29 28 3.14159265358979323846264338528130821901257632475497
60 30 29 3.14159265358979323846264338303346777076128203989348
62 31 30 3.14159265358979323846264338330975891422401062024213
64 32 31 3.14159265358979323846264338327578024251104640781263
66 33 32 3.14159265358979323846264338327996113286644931522925
68 34 33 3.14159265358979323846264338327944644909217865126224
70 35 34 3.14159265358979323846264338327950983738822780826626
72 36 35 3.14159265358979323846264338327950202716878513601036
74 37 36 3.14159265358979323846264338327950298987231150927805
76 38 37 3.14159265358979323846264338327950287116225420664830
78 39 38 3.14159265358979323846264338327950288580556599221706
80 40 39 3.14159265358979323846264338327950288399864216472867
82 41 40 3.14159265358979323846264338327950288422168158647707
84 42 41 3.14159265358979323846264338327950288419414198014964
86 43 42 3.14159265358979323846264338327950288419754341140003
88 44 43 3.14159265358979323846264338327950288419712318091733
90 45 44 3.14159265358979323846264338327950288419717511227961
92 46 45 3.14159265358979323846264338327950288419716869304890
94 47 46 3.14159265358979323846264338327950288419716948672353
96 48 47 3.14159265358979323846264338327950288419716938857050
98 49 48 3.14159265358979323846264338327950288419716940071172
N A T 11111111112222222222333333333344444444445
12345678901234567890123456789012345678901234567890
3.1415926535897932384626433832795028841971693993751
|
Let's see where the formula in the program above comes from, without any formal proof (although a proof would not be hard).
Here are the first set of averaging steps. Use s1[i] to denote the average of s[i] and s[i+1]. Similarly, use s2[i] to denote the average of s1[i] and s1[i+1], and so on for s3[i], etc.
The first set of averaging steps looks like the following.
The second set of averaging steps looks like:
s2[1] = (1/2)s1[1] + (1/2)s1[2] =
(1/2)((1/2)s[1] + (1/2)s[2]) + (1/2)((1/2)s[2] + (1/2)s[3]) =
(1/4)s[1] + (1/2)s[2] + (1/4)s[3]=
(1/4)(s[1] + 2 s[2] + s[3]),
s2[2] = (1/2)s1[2] + (1/2)s1[3] =
(1/2)((1/2)s[2] + (1/2)s[3]) + (1/2)((1/2)s[3] + (1/2)s[4]) =
(1/4)s[2] + (1/2)s[3] + (1/4)s[4]=
(1/4)(s[2] + 2 s[3] + s[4]), . . .
Then the third set of averaging steps start out:
s3[1] = (1/8)(s[1] + 3 s[2] + 3 s[3] + s[4]), . . .
Using the notation of the program above, this formula in general takes the form:
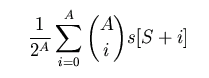
For A = 5 and S = 0, this formula takes the form:
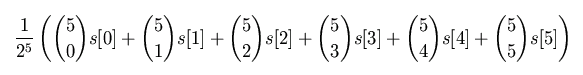
And then substituting for the expressions for combinations, it becomes:
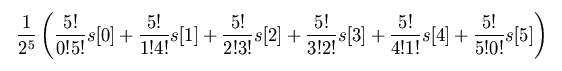
And finally, simplifying: