pi by continued fraction

Pi from a Continued Fraction

Calculating digits of pi using a continued fraction representation:

The Ruby release has a remarkably short and simple Ruby program that calculates arbitrarily many decimal digits of pi, using the continued fraction on the left:

Ruby program to calculate pi

The Formula used

#!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 4, 1, 12, 4
loop do
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  d, d1 = a/b, a1/b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end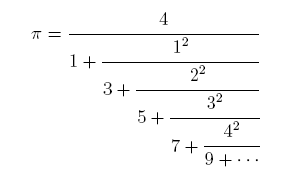

$PI as continued fraction$

Output of a run

% pi.rb
3141592653589793238462643383279502884 ...

How the algorithm for Pi works shows how this algorithm can be adapted to compute any continued fraction.

Here is an expanded verion that arranges the digits by 10s and in rows of 100. Given an optional command-line argument, it calculates pi to any base B <= 36.

Ruby program to calculate pi to any base

Output of runs

#!/usr/bin/env ruby
k, a, b, a1, b1 = 2, 4, 1, 12, 4
h = %w{0 1 2 3 4 5 6 7 8 9 a b c d e f g h
       i j k l m n o p q r s t u v w x y z}
if ARGV[0] == nil
  B = 10
else 
  B = ARGV[0].to_i
end 
dig = -1
row = -1
loop do
  # Next approximation
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  # Print common digits
  d = a / b
  d1 = a1 / b1
  while d == d1
    if dig == -1 then
       printf "     "
       print h[d]
       dig = dig+1
    else
       print h[d]
       dig = dig+1
    end
    if dig%10 == 0 then printf " " end
    if dig%100 == 0 then 
       row = row+1
       printf "\n%4i ", row
    end
    $stdout.flush
    a, a1 = B*(a%b), B*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end

% piA.rb
     3
   0 1415926535 8979323846 2643383279 ...
   1 8214808651 3282306647 0938446095 ...
% piA.rb 16
     3 
   0 243f6a8885 a308d31319 8a2e037073 ...
   1 29b7c97c50 dd3f84d5b5 b547091792 ...
% piA.rb 36
     3
   0 53i5ab8p5f sa5jhk72i8 asc47wwzla ...
   1 067iy9wnzd z9n4jltedt iw2b65acrp ...

Outputs of the above program:

spot

pi to 40000 decimal digits,
pi to 20000 hex digits,
pi to 10000 base 36 digits,
pi to 10000 base 62 digits (using 0-9,A-Z,a-z).

This program even works for bases 2 and 3, although it gives an initial digit in both cases of 3, the subsequent base 2 or base 3 digits are correct. (I checked base 2 against the hex digits and the initial few digits of base 3.)

Actually, this isn't a very efficient way to calculate pi, but it was able to give 5000 digits in 15 seconds and 10000 digits in under 60 seconds on a 800 Mhz Pentium.

Java version of the second Ruby program above:

BigInteger

Java program to calculate pi

import java.math.*; // for BigInteger
public class PiBig2 {

   public static void main(String[] args) {
      BigInteger TWO = new BigInteger("2");
      BigInteger TEN = new BigInteger("10");
      BigInteger k = new BigInteger("2");
      BigInteger a = new BigInteger("4");
      BigInteger b = new BigInteger("1");
      BigInteger a1 = new BigInteger("12");
      BigInteger b1 = new BigInteger("4");
      int dig = -1, row = -1;
      for (;;) {
         // Next approximation
         BigInteger p = k.multiply(k);
         BigInteger q = (TWO.multiply(k)).add(BigInteger.ONE);
         k = k.add(BigInteger.ONE);
         BigInteger tempa1 = a1;
         BigInteger tempb1 = b1;
         a1 = (p.multiply(a)).add(q.multiply(a1));
         b1 = (p.multiply(b)).add(q.multiply(b1));
         a = tempa1;
         b = tempb1;
         // Print common digits
         BigInteger d = a.divide(b);
         BigInteger d1 = a1.divide(b1);
         while (d.equals(d1)) {
            if (dig == -1) {
               System.out.print("     ");
               System.out.print(d);
               dig++;
            }
            else {
               System.out.print(d);
               dig++;
            }
            if (dig%10 == 0) System.out.print(" ");
            if (dig%100 == 0) {
               row++;
               System.out.println();
               if (row < 10) System.out.print("   " + row);
               else if (row < 100) System.out.print("  " + row);
               else if (row < 1000) System.out.print(" " + row);
               else System.out.print(row);
               System.out.print(" ");
            }
            a =  TEN.multiply(a.mod(b));
            a1 = TEN.multiply(a1.mod(b1));
            d = a.divide(b);
            d1 = a1.divide(b1);
         }
      }
   }
}

The continued fraction used throughout is a special case of a much more general formula:

$PI as continued fraction$

Plugging in z = 1 gives the previous formula. (See Wolfram Functions Pages.)

Revision date: 2005-12-21. (Use ISO 8601, an International Standard.)