PI: 3.1415926535...

Calculate Pi Inefficiently
Using Gregory's Series

Slow convergence to pi: Use the following formula:

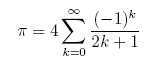
PI from a series

This is Gregory's series for pi. It just barely converges and would seem to be almost useless for serious and efficient computation of digits of pi.

A simple Java program: Here is a Java program that uses the above series to calculate pi:

Calculate Pi, slow convergence Output of a run, N = 1000
// PiSlow: pi from slowly converging series
public class PiSlow {
   public static final int N = 1000; // # of terms
   public static void main(String[] args) {
      double sum = 0.0;      // final sum
      double term;           // term without sign
      double sign = 1.0;     // sign on each term
      for (int k = 0; k < N; k++) {
         term = 1.0/(2.0*k + 1.0);
         sum = sum + sign*term;
         if (k%(N/50) == 0) // print one in 50
            System.out.println ("k: " + k + ", "
               + sum + ", pi: " + sum*4.0);
         sign = -sign;
      }
      System.out.println("Final pi/4 (approx., " +
         N + " terms): " + sum);
      System.out.println("Actual pi/4: " +
         Math.PI/4.0);
      System.out.println("Final pi (approx., " +
         N + " terms): " + sum*4.0);
      System.out.println("Actual pi: " + Math.PI);
   }
}

k: 0,   1.0,                pi: 4.0
k: 50,  0.7902996532467627, pi: 3.1611986129870506
k: 100, 0.7878733502677479, pi: 3.1514934010709914
k: 150, 0.7870537743844844, pi: 3.1482150975379377
k: 200, 0.7866419367957389, pi: 3.1465677471829556
k: 250, 0.7863941753814,    pi: 3.1455767015256
k: 300, 0.7862287258897132, pi: 3.1449149035588526
k: 350, 0.7861104126644118, pi: 3.1444416506576474
k: 400, 0.7860216038246902, pi: 3.144086415298761
k: 450, 0.7859524864411895, pi: 3.143809945764758
k: 500, 0.7858971648964472, pi: 3.143588659585789
k: 550, 0.7858518835320016, pi: 3.1434075341280066
k: 600, 0.7858141364872435, pi: 3.143256545948974
k: 650, 0.7857821877484866, pi: 3.1431287509939465
k: 700, 0.7857547965968966, pi: 3.1430191863875865
k: 750, 0.7857310527305843, pi: 3.142924210922337
k: 800, 0.785710273138507,  pi: 3.142841092554028
k: 850, 0.7856919353289389, pi: 3.1427677413157555
k: 900, 0.7856756327903573, pi: 3.1427025311614294
k: 950, 0.7856610445024891, pi: 3.1426441780099563
Final pi/4 (app., 1000 terms): 0.7851481634599485
Actual pi/4:                   0.7853981633974483
Final pi   (app., 1000 terms): 3.140592653839794
Actual pi:                     3.141592653589793

Surprising results: The results of a run with N = 1000 are on the right above. Notice that with 1000 terms, we still only get 3 significant digits of accuracy. These correct digits are shown in blue above and below. Incorrect digits are given in red. After the first incorrect digit come 6 more correct digits, shown in green. Then 2 more incorrect digits followed by 3 more correct ones. Of course this would be an unimaginably unlikely coincidence.

Here are results of runs with 4 values for N a power of 10. It's clear from these results that 10-digit accuracy of pi would require N = 1011, that is, 100000000000 terms.

Runs with N  a power of 10
Final pi (app., 100 terms):    3.1315929035595537
Actual pi:                     3.141592653589793

Final pi (app., 1000 terms):   3.140592653839794
Actual pi:                     3.141592653589793

Final pi (app., 10000 terms):  3.1414926535900345
Actual pi:                     3.141592653589793

Final pi (app., 100000 terms): 3.1415826535897198
Actual pi:                     3.141592653589793

The above results suggest that there are simple correction terms that would make the final sum much more accurate. These terms are shown on the next page. When I first ran these calculations, I noticed the clearly evident correction terms myself, but I knew that original work is unlikely in this area. In fact, the article about pi by Borwein talks about this issue in detail: The Life of Pi, by J.M. Borwein.

Here are calculations carried out in Mathematica to 100 digits:

Calculate Pi, slow convergence. 100-digit accuracy using Mathematica.
N = 1000000   0.785397913397448309678160845819797596049292588125026453891197085589288330087012285972929717092685565
Exact, pi/4   0.7853981633974483096156608458198757210492923498437764552437361480769541015715522496570087063355292670
N = 1000000   3.14159165358979323871264338327919038419717035250010581556478834235715332034804914389171886837074226
Exact, pi     3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068

N=10000000    0.785398138397448309615723345819875720268042349843800283368736146724415039071675591942164939839160859
Exact, pi/4   0.7853981633974483096156608458198757210492923498437764552437361480769541015715522496570087063355292670
N=10000000    3.14159255358979323846289338327950288107216939937520113347494458689766015628670236776865975935664344
Exact, pi     3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068

Notice how the red digits above could lead us to guess the correction terms. For N = 106 the first red digit shows that the sum differs from pi by (2-1)*10-6, so that the first corection term would be N-1 = 1/N.

The second set of red digits shows that the sum differs from pi by (71-46)*10-20 = 25*10-20 = 0.25*10-18, so that the second corection term would be -(1/4)*N-3 = -(1/4)/N3.

Similarly, the third correction term comes from: (5028-1903)*10-34 = (3125/10000)*10-30 = (5/16)*10-30. Thus the third correction term is (5/16)/N5.

Then the fourth correction term comes from: -(70352500-69399375)*10-48 = -(953125/1000000)*10-42 = -(61/64)*10-42. Thus the fourth correction term is -(61/64)/N7.

The last term we can get from this data starts with: (2097494459-1556478834)*10-62 = (541015625/100000000)*10-54 = (1385/256)*10-54. Thus the fourth correction term is (1385/256)/N9.

See better formulas for pi for a more on this formula.