

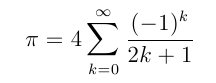
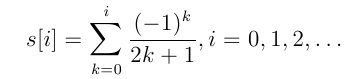
s[0] = 1 = 1/1 = 1.0000000; pi/4 - s[0] = -0.2146018 s[1] = s[0] - 1/3 = 1 - 1/3 = 2/3 = 0.6666666; pi/4 - s[1] = 0.1187314 s[2] = s[1] + 1/5 = 1 - 1/3 + 1/5 = 13/15 = 0.8666666; pi/4 - s[2] = -0.0812685 s[3] = s[2] - 1/7 = 1 - 1/3 + 1/5 - 1/7 = 76/105 = 0.7238095; pi/4 - s[3] = 0.0615886 s[4] = s[3] + 1/9 = 1 - 1/3 + 1/5 - 1/7 + 1/9 = 263/315 = 0.8349206; pi/4 - s[4] = -0.0495224 s[5] = s[4] - 1/11 = 2578/3465 = 0.7440115; pi/4 - s[5] = 0.0413866 s[6] = s[5] + 1/13 = 36979/45045 = 0.8209346; pi/4 - s[6] = -0.0355364 s[7] = s[6] - 1/15 = 33976/45045 = 0.7542679; pi/4 - s[7] = 0.0311302 s[8] = s[7] + 1/17 = 622637/765765 = 0.8130914; pi/4 - s[8] = -0.0276933 s[9] = s[8] - 1/19 = 11064338/14549535 = 0.7604599; pi/4 - s[9] = 0.0249382Since these values are flipping back and forth around pi/4, it seems as if the results would be much more accurate if we took the average of each pair of entries. Starting with s[0] and s[1], take the average of adjacent values, and overwrite the lower value with the new average. (This overwritten value doesn't participate in the later calculations.)
s[0] = (s[0] + s[1])/2 = 0.8333333; pi/4 - s[0] = -0.0479351 s[1] = (s[1] + s[2])/2 = 0.7666666; pi/4 - s[1] = 0.0187315 s[2] = (s[2] + s[3])/2 = 0.7952380; pi/4 - s[2] = -0.0098398 s[3] = (s[3] + s[4])/2 = 0.7793650; pi/4 - s[3] = 0.0060331 s[4] = (s[4] + s[5])/2 = 0.7894660; pi/4 - s[4] = -0.0040678 s[5] = (s[5] + s[6])/2 = 0.7824730; pi/4 - s[5] = 0.0029251 s[6] = (s[6] + s[7])/2 = 0.7876012; pi/4 - s[6] = -0.0022030 s[7] = (s[7] + s[8])/2 = 0.7836796; pi/4 - s[7] = 0.0017185 s[8] = (s[8] + s[9])/2 = 0.7867756; pi/4 - s[8] = -0.0013774Notice that because of the averaging, there is one fewer value in the list, so that s[9] is ignored afterward. These values are about a factor of 10 closer to pi/4, and they also flip back and forth around pi/4, so we could average adjacent values again, and yet again. The tables below show this averaging process taken a number of times. In the specific tables below, everything is multiplied by 4, so that the series is converging to pi. All values in the tables were stored as doubles in the program, but were truncated for display. These calculations wouldn't work at all without the full precition of a double. The column labeled "0" below gives the partial sums s[15] through s[31]. The column labeled "1" gives averages of adjacent elements from the "0" column. When entries for index i and i+1 are averaged, the result is stored in index i. At the end there is one fewer entry, and the resulting averages are stored under indexes 15 to 30. Then column "2" gives averages from column "1", and so on. Each time the averages are taken there is one fewer element, so that when we start with 17 elements, and after we average 16 times, there is only one element left. In this case, this final average gives pi accurate to 16 significant digits. This seems surprising to me. Using just the partial sums s[15] through s[31] and using repeated averaging gives 16 significant digits of pi.
| Pi by averaging. Each column gives successive numbers of times averaged. | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
15 3.0792 16 3.2004 17 3.0861 18 3.1942 19 3.0916 20 3.1892 21 3.0962 22 3.1850 23 3.0999 24 3.1816 25 3.1031 26 3.1786 27 3.1059 28 3.1761 29 3.1083 30 3.1738 31 3.1104 | 3.13976 3.14322 3.14013 3.14291 3.14040 3.14267 3.14061 3.14250 3.14076 3.14236 3.14088 3.14225 3.14098 3.14217 3.14106 3.14210 | 3.141491 3.141678 3.141520 3.141655 3.141539 3.141640 3.141552 3.141629 3.141561 3.141621 3.141567 3.141615 3.141572 3.141611 3.141576 | 3.1415847 3.1415991 3.1415875 3.1415969 3.1415891 3.1415956 3.1415902 3.1415947 3.1415909 3.1415942 3.1415913 3.1415938 3.1415917 3.1415935 | 3.14159186 3.14159326 3.14159218 3.14159302 3.14159236 3.14159289 3.14159246 3.14159281 3.14159253 3.14159276 3.14159257 3.14159273 3.14159259 | 3.141592559 3.141592722 3.141592603 3.141592692 3.141592624 3.141592676 3.141592636 3.141592667 3.141592643 3.141592662 3.141592647 3.141592659 | 3.1415926408 3.1415926625 3.1415926472 3.1415926582 3.1415926502 3.1415926561 3.1415926517 3.1415926550 3.1415926525 3.1415926544 3.1415926529 | 3.14159265165 3.14159265489 3.14159265270 3.14159265420 3.14159265316 3.14159265390 3.14159265337 3.14159265375 3.14159265347 3.14159265368 |
| Pi by averaging. Each column gives successive numbers of times averaged. | ||||
|---|---|---|---|---|
| 8 | 9 | 10 | 11 | 12 |
15 3.141592653267 16 3.141592653797 17 3.141592653454 18 3.141592653680 19 3.141592653528 20 3.141592653632 21 3.141592653560 22 3.141592653611 23 3.141592653575 | 3.1415926535320 3.1415926536255 3.1415926535673 3.1415926536043 3.1415926535803 3.1415926535962 3.1415926535855 3.1415926535928 |
15 3.1415926535787 16 3.1415926535964 17 3.1415926535858 18 3.1415926535923 19 3.1415926535882 20 3.1415926535908 21 3.1415926535891 | 3.14159265358755 3.14159265359108 3.14159265358904 3.14159265359025 3.14159265358951 3.14159265358997 | 3.14159265358932 3.14159265359006 3.14159265358964 3.14159265358988 3.14159265358974 |
| Pi by averaging. Each column gives successive numbers of times averaged. | 13 | 14 | 15 | 16 |
|---|---|---|---|
15 3.141592653589468 16 3.141592653589485 17 3.141592653589746 18 3.141592653589481 | 3.141592653589770 3.141592653589807 3.141592653589787 | 3.141592653589789 3.141592653589798 | 3.141592653589793 |
| Pi by averaging | Output of a run |
|---|---|
// PiAve: compute pi using inaccurate formula,
// followed by repeated averaging.
import java.text.DecimalFormat;
public class PiAve {
public static DecimalFormat d16 = new
DecimalFormat("0.0000000000000000");
public static String diff(double r) {
double t = (Math.PI) - r;
if (t < 0) return d16.format(t);
else return " " + d16.format(t);
}
public static void main(String[] args) {
// number of terms in the initial series
int N = Integer.parseInt(args[0]);
// number of times to average
int A = Integer.parseInt(args[1]);
if (A > N - 1) System.out.println("N too small");
double sum = 0.0; // cumulative sum
double term; // each term, without sign
double sign = 1.0; // sign of each term
double[] sums = new double[N]; // averaged values
// calculate N terms of inaccurate series for pi
for (int k = 0; k < N; k++) {
term = 1.0/(2.0*k + 1.0);
sum = sum + sign*term;
sign = -sign;
sums[k] = 4*sum;
}
// average adjacent pairs, processing A times
int M = N;
for (int dummy = 0; dummy < A; dummy++) {
for (int j = 0; j < M - 1; j++)
sums[j] = (sums[j] + sums[j + 1])/2.0;
M--;
}
// print final N - A values
for (int k = 0; k < N - A; k++)
System.out.println(k + " " + sums[k] +
" " + diff(sums[k]));
}
}
| % java PiAve 32 16 k sums[k] pi - sums[k] 0 3.1415930039365283 -0.0000003503467352 1 3.1415926263422733 0.0000000272475198 2 3.1415926569580237 -0.0000000033682306 3 3.1415926530329275 0.0000000005568657 4 3.141592653703066 -0.0000000001132729 5 3.141592653562805 0.0000000000269882 6 3.141592653597091 -0.0000000000072977 7 3.1415926535876073 0.0000000000021858 8 3.14159265359051 -0.0000000000007168 9 3.141592653589542 0.0000000000002509 10 3.141592653589889 -0.0000000000000959 11 3.1415926535897567 0.0000000000000364 12 3.1415926535898104 -0.0000000000000173 13 3.141592653589788 0.0000000000000053 14 3.1415926535897976 -0.0000000000000044 15 3.141592653589793 0.0000000000000000 % java PiAve 32 31 k sums[k] pi - sums[k] 0 3.141592653594113 -0.0000000000043201 % java PiAve 45 44 k sums[k] pi - sums[k] 0 3.1415926535897953 -0.0000000000000022 |
k sums[k] pi - sums[k] 26 3.1415926752780394 -0.0000000216882463 27 3.141592635502268 0.0000000180875253Here is the corresponding list of averaged values:
k sums[k] pi - sums[k] 0 3.141596660662465 -0.0000040070726719 1 3.1415925639045907 0.0000000896852024 2 3.141592658954716 -0.0000000053649227 3 3.1415926530639338 0.0000000005258594 4 3.1415926536606387 -0.0000000000708456 5 3.1415926535777956 0.0000000000119975 6 3.1415926535922165 -0.0000000000024234 7 3.1415926535892322 0.0000000000005609 8 3.1415926535899414 -0.0000000000001483 9 3.1415926535897523 0.0000000000000409 10 3.1415926535898078 -0.0000000000000147 11 3.1415926535897905 0.0000000000000027 12 3.1415926535897962 -0.0000000000000031 13 3.141592653589794 -0.0000000000000009In this case, even though the initial data is so very much better, it still took nearly as many averages to get 15 significant digits of pi.