PI: 3.1415926535...

Pi from a Continued Fraction
How the Algorithm Works
Pi and Other Constants, 40000 digits:
pi, e, phi, sqrt(2)

The algorithm, illustrated with a Ruby program:

    Below is a Ruby program that will produce arbitrarily many digits of pi, until one runs out of dynamic memory. It requires that Ruby supports arbitrarily large integer arithmetic, memory permitting. The program uses the infinite continued fraction expansion for pi at the right.

    Ruby program to calculate pi Continued Fraction Used
    #!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 4, 1, 12, 4
loop do
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  d, d1 = a/b, a1/b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end
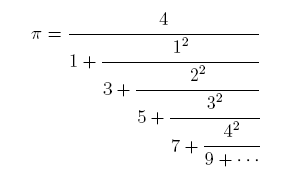    Output of a run
    % pi.rb
3141592653589793238462643383279502884 ...

    The algorithm as shown above is actually general-purpose and can be adapted to evaluate any continued fraction.

Producing pi without the individual digits:

    Keep just the first two lines inside the loop, and leave off the variables d, d1, and the entire inner loop.

    Truncated Ruby program
    #!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 4, 1, 12, 4
while k < 11
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  printf "k:%2i, a/b:%14i/%13i, pi:%18.12f\n",
     k, a, b, a.to_f/b.to_f
end
    Output of a run
    % pid.rb
k: 3, a/b:          12/4,          pi: 3.000000000000
k: 4, a/b:          76/24,         pi: 3.166666666667
k: 5, a/b:         640/204,        pi: 3.137254901961
k: 6, a/b:        6976/2220,       pi: 3.142342342342
k: 7, a/b:       92736/29520,      pi: 3.141463414634
k: 8, a/b:     1456704/463680,     pi: 3.141614906832
k: 9, a/b:    26394624/8401680,    pi: 3.141588825092
k:10, a/b:   541937664/172504080,  pi: 3.141593311880
k:11, a/b: 12434780160/3958113600, pi: 3.141592540447
    Convergents: partial evaluation of continued fraction

    In the program, k is the depth of iteration (after incrementing) of the continued fraction, p is k2, and q is 2*k + 1. Finally a and b give the numerator and denominator of the fraction that is the continued fraction to depth k, written as the quotient of two integers, without any reduction to lowest terms, and a1 and b1 are the a and b values at the next iteration. The fractions a/b and a1/b1 are called convergents, and they converge to the value of the infinite continued fraction.

A general continued fraction:

    A general infinite continued fraction might take the form on the left below, while the convergents are shown on the right:

    Then the following equations can be proven (using induction -- such proofs are in several places on the web, although not proving equations in exactly in this form). These equations allow easy calculation of the convergents. Of course the Ruby program just uses these, with almost the same notation. A normal programming language would have to keep track of three convergents, while Ruby with its multiple assignment statement allows one to work with an "old" a/b and a1/b1, and then "new" versions. Also the program only needs one p and one q at a time.

Showing the individual digits of pi produced:

    The first convergent is 4/1. The next two convergents are 12/4 and 76/24. (The first two convergents are assigned by initialization. All subsequent convergents are calculated using the formulas in the previous section.) When divided, using integer arithmetic, convergents 2 and 3 both yield 3, so a 3 (shown as bold red in the output below) would be output by the original program. (The program below commented out that simple output, and inserted three new print statements.) Now the 12/4 and the 76/24 each has the 3 that was output subtracted from it (using the % operator), and each is multiplied by 10 to get ready for the next output digit. And so it goes ...

Ruby program with extra outputOutput of a run
#!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 4, 1, 12, 4
while k < 9
  printf "k:%2i\n", k
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  # Print common digits
  d = a / b
  d1 = a1 / b1
  printf " Out:d:%i,d1:%i,p:%2i,q:%2i, a1/b1:%i/%i\n",
     d, d1, p, q, a1, b1
  while d == d1
    # print d
    # $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
    printf " In: d:%i,d1:%i,          a1/b1: %i/%i\n",
       d, d1, a1, b1
  end
end

k: 2
 Out:d:3,d1:3,p: 4,q: 5,a1/b1: 76/24
 In: d:0,d1:1,          a1/b1: 40/24
k: 3
 Out:d:1,d1:1,p: 9,q: 7,a1/b1: 280/204
 In: d:6,d1:3,          a1/b1: 760/204
k: 4
 Out:d:3,d1:4,p:16,q: 9,a1/b1: 9400/2220
k: 5
 Out:d:4,d1:4,p:25,q:11,a1/b1: 122400/29520
 In: d:2,d1:1,          a1/b1: 43200/29520
k: 6
 Out:d:1,d1:1,p:36,q:13,a1/b1: 748800/463680
 In: d:4,d1:6,          a1/b1: 2851200/463680
k: 7
 Out:d:6,d1:5,p:49,q:15,a1/b1: 49471200/8401680
k: 8
 Out:d:5,d1:5,p:64,q:17,a1/b1: 1023487200/172504080
 In: d:8,d1:9,          a1/b1: 1609668000/172504080

Other constants given by continued fractions:

    Here are several other constants given by continued fractions, as well as another one for pi:

Ruby program to calculate sqrt(2) Continued Fraction Used
#!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 3, 2, 7, 5
loop do
  p, q, k = 1, 2, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  d = a / b
  d1 = a1 / b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end
Output of a run
% sqrt2.rb
14142135623730950488016887242096980785696...

Ruby program to calculate e Continued Fraction Used
#!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 3, 1, 8, 3
loop do
  p, q, k = k, k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  d = a / b
  d1 = a1 / b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end
Output of a run
% sqrt2.rb
2718281828459045235360287471352...

Ruby program for phi (Golden Ratio) Continued Fraction Used
#!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 2, 1, 3, 2
loop do
  p, q, k = 1, 1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  d = a / b
  d1 = a1 / b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end
Output of a run
% sqrt2.rb
1618033988749894848204586834365...

Another program for e Continued Fraction Used
#!/usr/local/bin/ruby
k, a, b, a1, b1 = 2, 3, 1, 8, 3
loop do
  p, q, k = 1, 1, k+1
  if  k%3 == 2  then
    q = 2*(k+1)/3
  end
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  d = a / b
  d1 = a1 / b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end
Output of a run
% sqrt2.rb
2718281828459045235360287471352...

Here is another continued fraction to try:

Revision date: 2009-07-19. (Use ISO 8601, an International Standard.)