

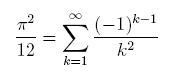
|
This well-known series still converges slowly, but certainly faster than Gregory's series.
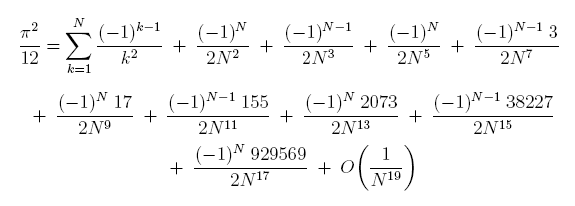
The coefficients in the numerators above (leaving off the first 1): 1, 1, 3, 17, 155, 2073, etc. are called Genocchi numbers (after an Italian mathematician). In some applications they have alternating signs, as is the case here.
The first 15 of these numbers are: 1, 1, 3, 17, 155, 2073, 38227, 929569, 28820619, 1109652905, 51943281731, 2905151042481, 191329672483963, 14655626154768697, 1291885088448017715, ... There are equations to generate these numbers.
| Calculate Pi, slow convergence. 100-digit accuracy using Mathematica. |
|---|
2 Exact, pi /12:0.8224670334241132182362075833230125946094749506033992188677791146850037352016004369168144503098793527 N=1000: 0.822466533924112718237707574823090093572994063638629128622478632373389371470175218659987899857060146 N=10000: 0.822467028424613218231207583473012586109475725603295568886892610037160176231995610724030713707422893 N=100000: 0.822467033374113718236207533323012609609474942103399226617779104320003754315100390438364594412973798 N=1000000: 0.822467033423613218736207583322512594609476450603399210367779114762503735200563936916833563809878888 N=10000000: 0.822467033424108218236707583323012589609474950603549218867779106185003735202375436916814346659879353 |
The second term is (2-7)*10-19 = -(1/2)*10-18, for a term of -(1/2)/N3.
The third term is (30-25)*10-31 = (1/2)*10-30, for a term of (1/2)/N5.
The fourth term is (49-64)*10-43 = -(3/2)*10-42, for a term of -(3/2)/N7.
The fifth term is (88-03)*10-55 = (17/2)*10-54, for a term of (17/2)/N9.
The sixth term is (6850-7625)*10-67 = -(155/2)*10-66, for a term of -(155/2)/N11.
The seventh term is (16004-05639)*10-79 = (2073/2)*10-78, for a term of (2073/2)/N13.
The eigth term is (144503-335638)*10-91 = -(38227/2)*10-90, for a term of -(38227/2)/N15.
| Calculate Pi Using Genocchi Terms |
|---|
// Genocchi: compute pi approximately
import java.text.DecimalFormat;
public class Genocchi {
public static DecimalFormat d16 = new
DecimalFormat("0.0000000000000000");
public static void main(String[] args) {
double N = Integer.parseInt(args[0]);
double sum = 0.0; // final sum
double term; // each term, without sign
double sign = 1.0; // sign on each term
for (int k = 1; k <= N; k++) {
term = 1.0/k/k;
sum += sign*term;
sign = -sign;
}
// assuming that N is even
// for odd N, reverse all signs below
System.out.println("0: " + d16.format(sum));
sum += 1.0/2/N/N;
System.out.println("1: " + d16.format(sum));
sum -= 1.0/2/N/N/N;
System.out.println("2: " + d16.format(sum));
sum += 1.0/2/N/N/N/N/N;
System.out.println("3: " + d16.format(sum));
sum -= 3.0/2/N/N/N/N/N/N/N;
System.out.println("4: " + d16.format(sum));
sum += 17.0/2/N/N/N/N/N/N/N/N/N;
System.out.println("5: " + d16.format(sum));
sum -= 155.0/2/N/N/N/N/N/N/N/N/N/N/N;
System.out.println("6: " + d16.format(sum));
sum += 2073.0/2/N/N/N/N/N/N/N/N/N/N/N/N/N;
System.out.println("7: " + d16.format(sum));
sum -= 38227.0/2/N/N/N/N/N/N/N/N/N/N/N/N/N/N/N;
System.out.println("8: " + d16.format(sum));
System.out.println("p: " +
d16.format(Math.PI*Math.PI/12));
}
}
|
| N = 2 | N = 4 | N = 6 | N = 8 | N = 10 | |
|---|---|---|---|---|---|
0 1 2 3 4 5 6 7 8 | 0.7500000000000000 0.8750000000000000 0.8125000000000000 0.8281250000000000 0.8164062500000000 0.8330078125000000 0.7951660156250000 0.9216918945312500 0.3383941650390625 | 0.7986111111111112 0.8298611111111112 0.8220486111111112 0.8225368923611112 0.8224453396267362 0.8224777645534940 0.8224592871136136 0.8224747321671910 0.8224569313331611 | 0.8108333333333334 0.8247222222222222 0.8224074074074075 0.8224717078189301 0.8224663494513031 0.8224671928980593 0.8224669792800083 0.8224670586402627 0.8224670179892410 | 0.8156164965986396 0.8234289965986396 0.8224524340986396 0.8224676928877020 0.8224669776319647 0.8224670409618998 0.8224670319397124 0.8224670338250949 0.8224670332818566 | 0.8179621756109852 0.8229621756109852 0.8224621756109852 0.8224671756109853 0.8224670256109853 0.8224670341109853 0.8224670333359854 0.8224670334396353 0.8224670334205219 |
| N = 12 | N = 14 | N = 16 | N = 18 | N = 20 | |
|---|---|---|---|---|---|
0 1 2 3 4 5 6 7 8 | 0.8192821939764581 0.8227544161986803 0.8224650643468284 0.8224670737346885 0.8224670318724414 0.8224670335197983 0.8224670334154927 0.8224670334251802 0.8224670334239397 | 0.8200973129234452 0.8226483333316085 0.8224661175881682 0.8224670472603286 0.8224670330306527 0.8224670334420550 0.8224670334229172 0.8224670334242230 0.8224670334241001 | 0.8206355073678897 0.8225886323678897 0.8224665620553897 0.8224670388925479 0.8224670333046125 0.8224670334283037 0.8224670334238984 0.8224670334241285 0.8224670334241120 | 0.8210092952272601 0.8225525051038033 0.8224667712217731 0.8224670358325201 0.8224670333824207 0.8224670334252722 0.8224670334240662 0.8224670334241160 0.8224670334241131 | 0.8212793783297532 0.8225293783297531 0.8224668783297532 0.8224670345797532 0.8224670334078782 0.8224670334244798 0.8224670334241014 0.8224670334241141 0.8224670334241135 |