PI: 3.1415926535...

Gregory's Series
with Extra Correction Terms

Better Formulas involving Gregory's series: An earlier page derived all but the last two terms of the formula below. This was only an empirical discovery of the formula, and not a proof, but often it is a good start to know what you are trying to prove. Here is a general version of this formula with two more terms:

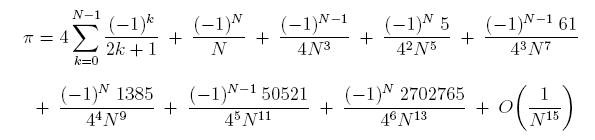
As detailed in the writeup The Life of Pi, by J.M. Borwein, the numbers in the numerators of each term above, namely, 1, -1, 5, -61, 1385, -50521, 2702765, ... are called Euler numbers because they were discovered and extensively studied by the great Swiss mathematician Leonhard Euler. The calculations below illustrate these formulas.

Here is a simple Java program that uses the terms of the series above to calculate pi:

Calculate Pi Using Euler Terms
// Euler: compute pi approximately
import java.text.DecimalFormat;
public class Euler {
   public static DecimalFormat d16 = new
                 DecimalFormat("0.0000000000000000");
   public static void main(String[] args) {
      double N = Integer.parseInt(args[0]);
      double sum = 0.0;      // final sum
      double term;           // each term, without sign
      double sign = 1.0;     // sign on each term
      for (int k = 0; k < N; k++) {
         term = 1.0/(2.0*k + 1.0);
         sum += sign*term;
         sign = -sign;
      }
      sum *= 4.0;
      // assuming that N is even
      // if N is odd, reverse all signs below
      System.out.println("0: " + d16.format(sum));
      sum += 1.0/N;
      System.out.println("1: " + d16.format(sum));
      sum -= 1.0/4/N/N/N;
      System.out.println("2: " + d16.format(sum));
      sum += 5.0/16/N/N/N/N/N;
      System.out.println("3: " + d16.format(sum));
      sum -= 61.0/64/N/N/N/N/N/N/N;
      System.out.println("4: " + d16.format(sum));
      sum += 1385.0/256/N/N/N/N/N/N/N/N/N;
      System.out.println("5: " + d16.format(sum));
      sum -= 50521.0/1024/N/N/N/N/N/N/N/N/N/N/N;
      System.out.println("6: " + d16.format(sum));
      sum += 2702765.0/4096/N/N/N/N/N/N/N/N/N/N/N/N/N;
      System.out.println("7: " + d16.format(sum));
   }
}

Here are results of a run with different values of N in different columns. The labels 0 through 7 on the rows give the number of extra correction terms added in. The correct digits are in green. With N = 18, the full formula gives 15 significant digits of accuracy. With odd values for N, and with the signs in the program reversed, the results are consistent with those below.

N = 2N = 4N = 6N = 8N = 10 
0
1
2
3
4
5
6
7

2.6666666666666670
3.1666666666666670
3.1354166666666670
3.1451822916666670
3.1377360026041670
3.1483027140299480
3.1242124239603680
3.2047610978285475

2.8952380952380956
3.1452380952380956
3.1413318452380956
3.1416370210193456
3.1415788468860450
3.1415994849942983
3.1415877221573503
3.1415975547591410

2.9760461760461765
3.1427128427128430
3.1415554353054356
3.1415956230626370
3.1415922182665410
3.1415927551110987
3.1415926191207060
3.1415926696428860

3.0170718170718180
3.1420718170718180
3.1415835358218180
3.1415930725649820
3.1415926180795655
3.1415926583883707
3.1415926526447980
3.1415926538450667

3.0418396189294032
3.1418396189294033
3.1415896189294035
3.1415927439294036
3.1415926486169035
3.1415926540270600
3.1415926535336904
3.1415926535996760

N = 12 N = 14N = 16N = 18N = 20
0
1
2
3
4
5
6
7
3.0584027659273330
3.1417360992606667
3.1415914233347406
3.1415926792021533
3.1415926526021840
3.1415926536507084
3.1415926535843070
3.1415926535904740

3.0702546177791854
3.1416831892077570
3.1415920813360367
3.1415926623811368
3.1415926533393637
3.1415926536012164
3.1415926535890333
3.1415926535898646

3.0791533941974280
3.1416533941974280
3.1415923590411780
3.1415926570644017
3.1415926535137344
3.1415926535924625
3.1415926535896580
3.1415926535898047

3.0860798011238346
3.1416353566793900
3.1415924897383750
3.1415926551200917
3.1415926535632575
3.1415926535905320
3.1415926535897643
3.1415926535897960

3.0916238066678400
3.1416238066678397
3.1415925566678395
3.1415926543240897
3.1415926535794610
3.1415926535900276
3.1415926535897870
3.1415926535897950