CS 3723 Programming Languages   Fall 2014
Homework 4. NFAs with ε-moves
Week 4: Sep 15 - 19

Submit following directions at: submissions and rules at: rules. Deadlines are: 2014-09-29  23:59:59 (that's Mon, 29 Sep 2014, 11:59:59 pm) for full credit. 2014-10-03  23:59:59 (that's Fri,     3 Oct 2014, 11:59:59 pm) for 75% credit.

Note: Extra problem number 4 added at the end on 2014-09-23.
  (But hey, I also deleted the last two problems on Homework 5.)

Also, there's now a hint on Problem 3.

1. Use the following NFA to represent the RE: /(aa)*(bb)*/. Carry out the extended subset algorithm on this NFA to get a DFA that accepts the same language. This isn't the only NFA that will work, but this is the one you must work with. [The answer has 5 states, including the state corresponding to the empty set, that is, the error state.] The "Questions" page gives a big hint about this problem. Please try to do the problem before looking at the hint.
   

2. Suppose you want to handle the regular expression: /ab(ab)*/. The figure below gives this converted to an NFA with ε-moves. (Here "@" is what I use for ε in programs (ε = the empty string). This isn't the only NFA that will work, but this is the one you must work with. (Below, the transition from state 7 to state 9 should be labeled with @.)
   
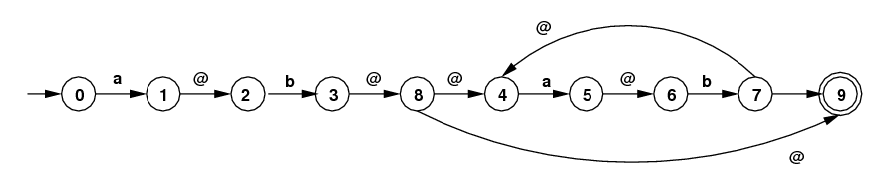
   1. Carry out the extended subset algorithm on this NFA to get a DFA that accepts the same language. [Your answer should have 6 states including the empty set as an error state.]

   2. This DFA is not optimal: it doesn't have the minimal number of states. But it can be converted to that optimal DFA by identifying two pairs of its states: the two terminal states (there are only 2), and two of the non-terminals. See if you can figure out what the minimal DFA is. (You haven't been given an algorithm for this.)

3. For this problem, you are to write another function p with one parameter n. This function must evaluate the same fraction, but must do it top-down, rather than bottom-up as before. You must use recursion and it must work for general n. The function cannot have a loop in it. Give results for p(10), p(15) and p(20). [This function should be short. It's possible to write the function so that it contains no assignment statements, though this is not a requirement. Remember that a recursive function cannot call itself recursively first, but must first check for a special case that terminates the recursion.]
   [Hint: I wouldn't normally give a hint for this problem, but on Friday (Sep 26) I "explained" the problem exactly upside down, making things too confusing. So the idea is to define a "helper" function q, where q has a parameter n, say. Calling q with input parameter value 1 should give the part of the fraction starting with
   1 + 1²/(3 + ...),

   that is, the main denominator of the fraction (down to some level L). The final value we want will be 4/q(1).

   Similarly, calling q with input parameter 2 should give the part of the fraction starting with

   3 + 2²/(5 + ...),

   and so forth. The function q should calculate the initial part directly and finish off with a recursive call using parameter one bigger. When the input parameter gets up to some limiting value (say, 15), you have to terminate the recursion.

Step 1: Parser: Here (a|b|c)* is translated to RPN form: ab|c|*

Step 2. Translate to NFA with ε-moves: Here the following NFA with ε-moves would be constructed. Refer to the page: RE−−>NFA.

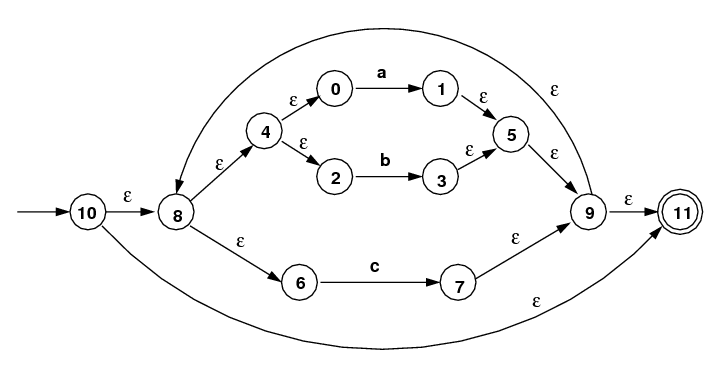Here is the internal representation of the above graph. This information is not needed for this problem.

Graph (internal form)
State Adjacency List 0 --> [a, 1] 1 --> [@, 5] 2 --> [b, 3] 3 --> [@, 5] 4 --> [@, 2] --> [@, 0] 5 --> [@, 9] 6 --> [c, 7] 7 --> [@, 9] 8 --> [@, 6] --> [@, 4] 9 --> [@, 8] --> [@,11] s 10 --> [@,11] --> [@, 8] t 11 -->

Step 4b. NFA Simulator (skip Step 3): The table below shows the output of the simulator. Here there are 12 states, numbered from 0 to 11. The start state is 10 and the only terminal state is 11. The subsets of the set of states are represented by "bit"-strings of length 12, where a 0 means the state is not in the subset and a 1 means the state is in the subset. (I cheated; they are actually char strings.) The position numbers (from 0 to 11) are given first across the top. Next comes a row representing the start state alone. After that is a row giving the ε-closure of the start state. Then comes the state resulting from processing an input "a".

Auto: start: 10, term: 11
Total states: 12
abcab$
execNFA: execStr: abcab$

 |                     1 1 
 | 0 1 2 3 4 5 6 7 8 9 0 1 
 | - - - - - - - - - - - - 
 : 0 0 0 0 0 0 0 0 0 0 1 0  s
 : 1 0 1 0 1 0 1 0 1 0 1 1  st
a: 1 1 1 0 1 1 1 0 1 1 0 1  t

4. 1. Verify that the Start State of the Simulated NFA is correct. (This is the next-to-the-last line, with "st" at the end.) [As an answer you can just do "mumble-mumble go from here to there", or better (but not required) show roughly how the depth-first search would proceed.]

   2. Verify that the last line is correct. This is the subset resulting from processing an input "a". (You must "show your work", meaning that you must give the set of states you find as being at the head of arrows labeled "a", and then show the result of the ε-closure.)

   3. Calculate the next two lines by hand, assuming the further inputs (after the initial "a") are "b" and then "c". Give the resulting lines. (Again, in these two cases you must "show your work" as above.)

( Revision date: 2014-09-23. Please use ISO 8601, the International Standard Date and Time Notation.)