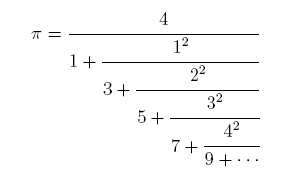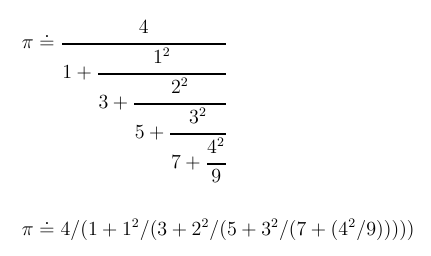| |
|
|
CS 3723
Programming Languages
Fall 2014 |
Homework 2. Subset Algorithm
|
Week 2: Sep 3 - 5
|
Submit following directions at:
submissions
and rules at:
rules.
Deadlines are:
- 2014-09-15 23:59:59 (that's Mon, 15 Sep 2014, 11:59:59 pm)
for full credit.
- 2014-09-19 23:59:59 (that's Fri, 19 Sep 2014, 11:59:59 pm)
for 75% credit.
|

Under Construction
Subset Algorithm:
Read the page Subset Algorithm.
You must understand how this algorithm works and be able to
carry it out "by hand" (not using a program).
In the three problems below, you must use the subset algorithm,
and you must show your work.
You don't need to draw a diagram of
the DFA resulting from using the subset algorithm.
(You should draw a diagram for your private use in seeing if
you seem to have the right answer.)
Your answers can look like the
items in the link above identified as "Tables" and
labeled "DFA". Don't write a table for the input NFA.
- Use the subset algorithm to convert the following NFA
into a DFA that accepts the same language.
(Hint: The DFA also has 4 states.)
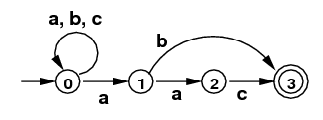
NFA for
/(a|b|c)*(ab|aac)/
(Intuitively, any string of "a"s, "b"s, and "c"s,
ending in "ab" or "aac".)
- Use the subset algorithm to convert the following NFA
into a DFA that accepts the same language.
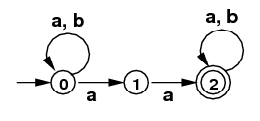
NFA for
/(a|b)*(aa)(a|b)*/
(Intuitively, any string of "a"s, and "b"s,
containing "aa" somewhere.)
Note: You must use the subset algorithm, and your answer must
be what that algorithm generates. (It turns out that the
minimal DFA for this language has one fewer state than the
result of the algorithm.)
- Use the subset algorithm to convert the following NFA into a DFA
that accepts the same language.
(Hint: Unlike 1 and 2 above, here you need the empty set Ø
as one of your subsets, since an initial b is not allowed
in this case.)
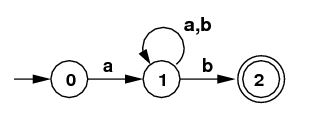
NFA for
/a(a|b)*b/
(Intuitively, an "a", followed by any string
of "a"s, and "b"s,
followed by a "b")
Continued Fraction Evaluation:
For this part you are to write Python code to evaluate
the following "weird" fraction (called a continued
fraction). The resulting code will be used later in the course.
(This code should be simple, not using any special features
of Python. A C version would look almost the same.)
So what does it mean to "evaluate" this? Can we use three dots in
our code? No, of course not. Just as with an "infinite" series,
we evaluate finite initial portions and take the limit as the
initial portions get ever larger ("tend to infinity"). Here is
what an initial portion could look like if we stop at "9".
(We drop everything from that point on.)
The second line shows the same fraction written with parentheses.
Of course you could use the second expression directly in a
program (with 42 replaced by 4*4 etc.).
Instead you should use a loop to evaluate this step-by-step, proceeding
from the bottom to the top.
Here is a general version of the fraction truncated at position n
for some integer n
- For this part of the homework, write a Python function that
has a parameter n and that evaluates the expression
from the bottom up, using a loop.
Give the values of p(10) and p(15).
[You must use a loop, so that it would work for any n.
Later you will be asked to use a top-down approach and recursion,
but you should not use recursion here.]
( Revision date: 2014-08-28.
Please use ISO
8601, the International Standard.)
|