CS 3723
 Programming Languages 
  NFAs with ε Moves  

Introduction. You should first study the web pages:

NFAs with ε moves: Here one allows transitions labeled with ε, the empty string. This means that you can follow such an arrow without consuming any input symbols. The NFA on the left shows how useful epsilon moves are in recognizing regular expressions with the example a*b*c*: which is "zero of more as, followed by zero or more bs, followed by zero of more cs". (The diagram uses "eps" for ε.)

On the right is a DFA that recognizes the same language. Notice some new things about this DFA: three states are terminal ones, including the start state. There is an "error" state, with label the empty set Ø, and it is not terminal. If you transition to that state, you can't get out and you can't accept. This state could also have been labeled as: error. The empty set can also be denoted by { }.

A refinement or expansion of the Subset Algorithm shows how to construct this DFA.


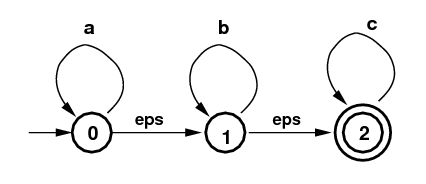
NFA for a*b*c*

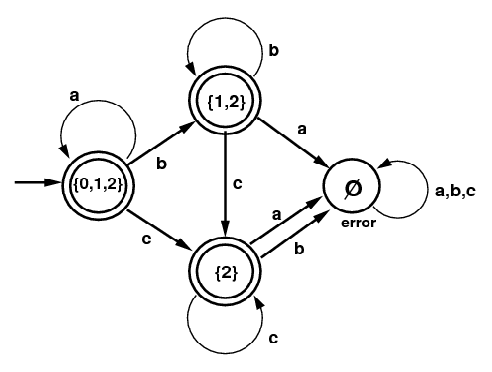
DFA for a*b*c*
Subset Algorithm (Tables)
DFA, a*b*c*
Statesabc
  {0,1,2} (start,term) {0,1,2}{1,2}{2}
  {1,2} (term) Ø{1,2}{2}
  {2} (term) ØØ{2}
  Ø ØØØ

ε-closure: The key to constructing a DFA from an NFA with ε-moves is the ε-closure algorithm. The starts with a set of states and find all additional states that can be reached from the given states using ε-moves. The algorithm below uses a stack to carry out a depth-first search. We could just as well have used a queue instead of a stack, and carried out a breadth-first search, since the order of visiting nodes doesn't matter in this case.

Algorithm: ε-closure
Input: an NFA with ε-moves N, a set P of states.
Output: ε-closure(P), which is P along with all   
   states reachable from P by a sequence of ε-moves.
Method: use stack S to carry out a depth-first search
// black means in ε-closure(P)
color all states white
color all states of P black
push all states of P onto S
while (S not empty) {
   u = pop(S)
   for (each edge (u,v) labeled ε) {
      if (v has color white) {
         color v black
         push v onto S
      }
   }
}
ε-closure(P) = black states
   
The subset algorithm for an NFA with ε-moves is the same as the one for ordinary NFAs, except that each time a subset is constructed, it must have the ε-closure algorithm (at the left) applied to it.

In the above case, the start state of the NFA is 0, so the start state of the DFA is not {0} but ε-closure({0}) = {0,1,2}.

Transitions on b from 0, 1, or 2 only go to 1. Then ε-closure({1}) = {1,2}.

There are no transitions on a from 1 or 2, so the set in this case is Ø, the empty set. The empty set is a subset that serves as an error state.

Large Example: Let's look at a more complicated example:

This is the NFA generated for the RE: "(a|b|c)*(ab|aac)" . Converting this to a DFA may be a homework problem.

(Revision date: 2014-09-16. Please use ISO 8601, the International Standard.)