CS 3723
 Programming Languages 
  RE −−> NFA  

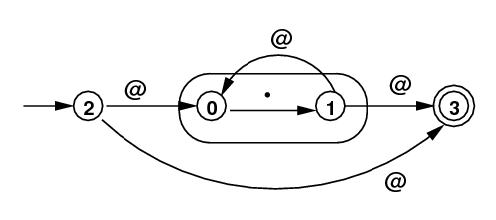
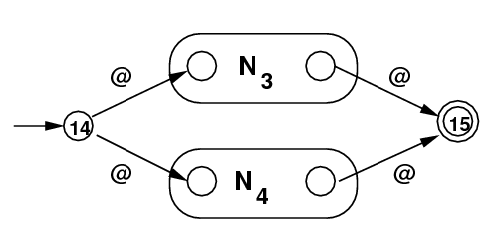
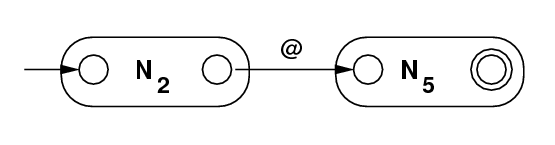
Regular Expression −−> NFA with ε-moves: Given an arbitrary regular expression R, it describes a language, that is, a set of strings of symbols over some alphabet. From R, we want to create an NFA with ε-moves called N so that N accepts any string described by R and rejects any other string. Then we would implement N with a program. The result a regular expression recognizer.

First we will translate R into RPN notation, including an explicit concatenation operator +. This allows us to break R up into a sequence of elementary steps, each one using a single operator. Then we handle the operators one-at-a-time to translate to N. The table below shows how this can be done, with each component regular expression on the left and the corresponding NFA on the right.

Regular
Expression		 NFA with ε-moves
Constructed

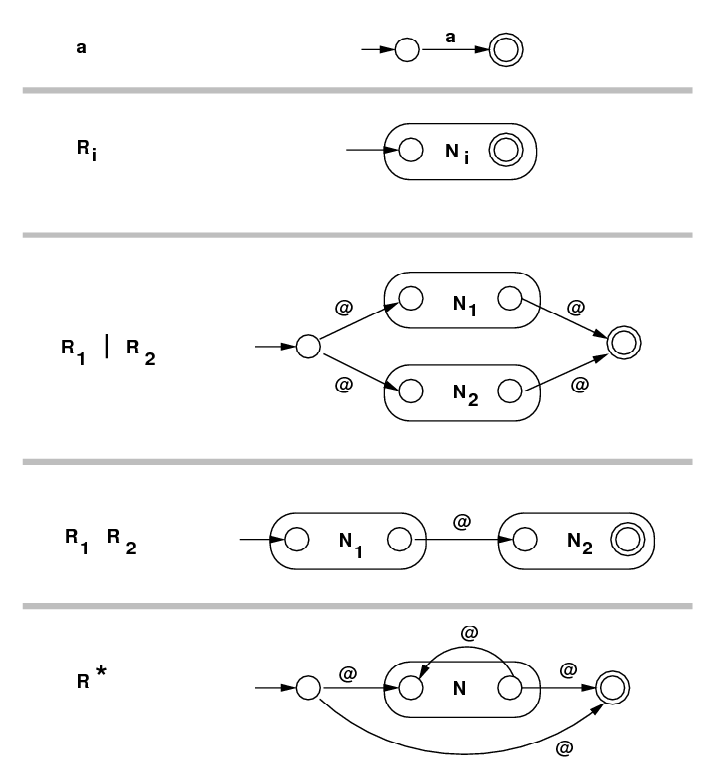
Specific Example: In the rest of this page, I'll focus on a specific regular expression. Suppose we want to use the RE (ab|aac). First concatenate .* at the left to get:

    R = ".*(ab|aac)$"

Why are we doing this?

Example (Overview): Here is a sequence of regular expressions, bulding up R one operation at a time (in several cases two operations are combined together below):

Regular ExpressionNFA
Name		 NFA with ε-moves
 R1 = .
 (matches any
  symbol)		  N1 
 R2 = R1*
 (star operator)		  N2 
 R3 = ab
 (concatenation)		  N3 
 R4 = aac
 (concatenation
  twice)		  N4 
Regular
Expression		NFA
Name		 NFA with ε-moves
 R5 = R3 | R4 
 (or operator)		  N5 
 R = R2R5
 (concatenation)		  N 

Example (Creating the NFA):

  • Regular Expression:   .*(ab|aac)$
  • RPN Form or Regular Expression:   .*ab+aa+c+|+$

Input
Processed		 NFA
(so far)		 Edges
Added		 NFA
(graph representation)		Controlling
Stack
. 
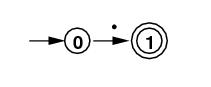 0 .  1
 
 0 --> [., 1]
 1
 
[0, 1](top)
.* 
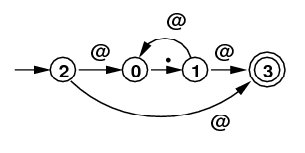 1 @  0
 1 @  3
 2 @  3
 2 @  0
 
 0 --> [., 1]
 1 --> [@, 0] --> [@, 3]
 2 --> [@, 3] --> [@, 0]
 3
 
[2, 3](top)
.*ab+ 
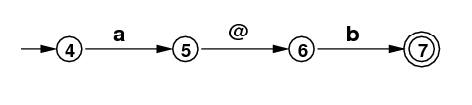 4 a  5
 6 b  7
 5 @  6
 
 4 --> [a, 5]
 5 --> [@, 6]
 6 --> [b, 7]
 7
 
[4, 7](top)
[2, 3]
.*ab+aa+c+
    (2 steps)		 
 8 a  9
10 a 11
 9 @ 10
12 c 13
11 @ 12
 
 8 --> [a, 9]
 9 --> [@,10]
10 --> [a,11]
11 --> [@,12]
12 --> [c,13]
13
 
[8,13](top)
[4, 7]
[2, 3]
.*ab+aa+c+|+
    (2 steps)
 
 7 @ 15
13 @ 15
14 @  4
14 @  8
 3 @ 14
 
 0 --> [., 1]
 1 --> [@, 0] --> [@, 3]
 2 --> [@, 3] --> [@, 0]
 3 --> [@,14]
 4 --> [a, 5]
 5 --> [@, 6]
 6 --> [b, 7]
 7 --> [@,15]
 8 --> [a, 9]
 9 --> [@,10]
10 --> [a,11]
11 --> [@,12]
12 --> [c,13]
13 --> [@,15]
14 --> [@, 8] --> [@, 4]
15 --> 
[2,15](top)

Example (Simulating the NFA): You'll be using my software to do this simulation.

  • Input String to Match:   cabcaaacabac$

NFA
(graph representation)		 Simulation
Trace
Reg. Expr: .*(ab|aac)$
RPN Form: .*ab+aa+c+|+$
The NFA as a graph:
 0 --> [., 1]
 1 --> [@, 0] --> [@, 3]
 2 --> [@, 3] --> [@, 0]
 3 --> [@,14]
 4 --> [a, 5]
 5 --> [@, 6]
 6 --> [b, 7]
 7 --> [@,15]
 8 --> [a, 9]
 9 --> [@,10]
10 --> [a,11]
11 --> [@,12]
12 --> [c,13]
13 --> [@,15]
14 --> [@, 8] --> [@, 4]
15 --> 

Input string to match:
cabcaaacabac$
Successive sets of states:
 |                     1 1 1 1 1 1 
 | 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 
 | - - - - - - - - - - - - - - - - 
 : 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 s
 : 1 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 s
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
b: 1 1 0 1 1 0 0 1 1 0 0 0 0 0 1 1 t
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0  
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 1 1 1 t
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
b: 1 1 0 1 1 0 0 1 1 0 0 0 0 0 1 1 t
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0

Example (Without ε-moves:) Here is the final NFA with ε-moves (called N above) written in a simple way as an NFA without ε-moves. It will be a recitation exercise to transform this into a DFA that accepts the same language.

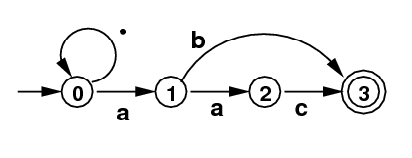
Example (Details about creating the NFA): [To be filled in.]

 

Revision date: 2014-08-30. (Please use ISO 8601, the International Standard.)