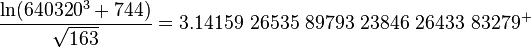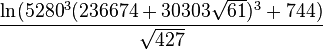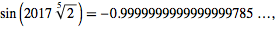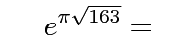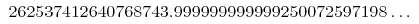Python 13.1 Arbitrary-Precision Float

• mpmath: a third-party addition to Python, this seems the best choice.
  • I installed it on my Linux and on my Mac system at home with no trouble, downloading it from online links. The package works for Python 2.5 or higher, including Python 3.x. My install required root privileges.

  • It is also available for Windows, but I couldn't try that. (No Windows!)

  It is pure-Python code, and seems very sophisticated, with a lot of fancy capabilities and features. See also mpmath docs. I tested both the Linux and the Mac OSX versions.

• Others: Python has other such arbitrary-precision float libraries, as do C and Lisp and many others.

# mpmath_test.py
from mpmath import *
import sys

mp.dps = 50 # 50 digit calculations
print "Precision: ", mp.dps
print mpf(2)**mpf('0.5') # sqrt(2)
print 2*pi # 2*pi
near_int = e**(pi*mpf(163)**mpf('0.5'))
print near_int # very close to an int

% Python mpmath.py
Precision:  50
1.4142135623730950488016887242096980785696718753769
6.2831853071795864769252867665590057683943387987502
262537412640768743.99999999999925007259719818568887

         1         2         3         4         5
12345678901234567890123456789012345678901234567890

(all digits above are correct)

Next are two formulas giving π accurate to 30 and to 52 decimals.

# tmp.py
from mpmath import *
import sys

mp.dps = 80
print "Precision: ", mp.dps
pi_approx = mp.log(mpf(640320) ** 3 + mpf(744)) / mp.sqrt(163)
print pi_approx

pi_approx2 = mp.log( (mpf(5280) * (mpf(236674) + mpf(30303) * \
      mp.sqrt(mpf(61)))) ** 3 + mpf(744)) / mp.sqrt(mpf(427))
print pi_approx2
print pi

% Python tmp.py
Precision:  80
3.1415926535897932384626433832797266193475498808835224222929628774422587390510494
3.1415926535897932384626433832795028841971693993751058600689073618724169264129391
3.141592653589793238462643383279502884197169399375105820974944592307816406286209

           1         2         3         4         5         6         7         8
  12345678901234567890123456789012345678901234567890123456789012345678901234567890

Try these (the second one is my own "discovery"):

Items of Interest or for study (see mpmath docs):

• Instead of  from mpmath import *  you can use  import mpmath  at the head, but then you need to add  mpmath.  at the start of the references to the library.

• mp.dps=50  declares the precision to be 50 decimal digits. You can change this precision any time in the program. You should realize that this is a floating point number, represented internally in binary. The phrase "50 decimal digits of precision" means enough significant binary digits to be the equivalent of 50 decimal digits. Using formulas at the start of Section 13.3, 50 decimal digits means the equivalent of 50/log₁₀(2) = 50/0.30103 = 166.1 binary digits (bits). Separate from this is a exponent in binary which can truly be almost arbitrarily large. The mpmath package supports a very large number of operations on these arbitrarily large floats, which can be thousands of digits long,

• mpf(2)  declares a high-precision constant with value 2. Notice from the mpmath docs that  mpf(10.1)  doesn't work correctly, while  mpf('10.1')  does. This is because the constant 0.1 has no exact representation as a double within the binary mpmath, So instead of starting from 0.1 as a double, one needs to have  mpmath  construct its own representation of  0.1  from scratch. By the same logic,  mpf(0.5)  does work.

• The software works with ordinary arithmetic operators and with ordinary integer constants. (I've sometimes changed an integer constant to multi-precision form when it wasn't required.)

• There are often alternatives to ordinary operators, as with:

  Instead of ...	you can write:
  e ** (...)	mp.exp(...)
  (...) ** mpf('0.5')	mp.sqrt(...)

• Determining error bounds is important and hard to do. I haven't been bothering with this, and I'm sticking to problems where I already know the correct answer.

(Revision date: 2018-09-31. Please use ISO 8601, the International Standard.)