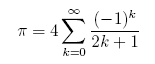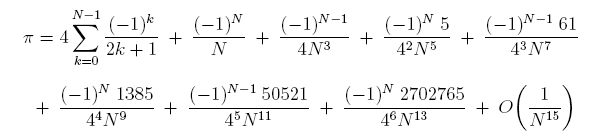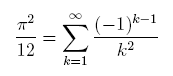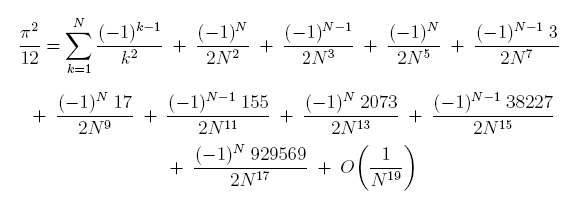| |
 |
|
Python |
13.2 Gregory's Series
|
|
Gregory's Series:
Here we're showing a larger calculation: sums of Gregory's series,
using the formula below. These sums are computed with up to 100-digit
accuracy (and much higher accuracy at the end of this section),
using Python, with the mpmath extension. (I've carried
out many of these high precision
calculations on Mathematica and clisp,
getting exactly the same results.)
|
mpmath: More Sample Calculations |
|---|
| Ordinary Python |
Python with mpmath |
|---|
# greg.py: Gregory's series
# for doubles
from __future__ import print_function
N = 100
sum = 0.0
sign = 1
for k in range(0,N):
term = 1.0/(2.0*k + 1.0)
sum = sum + sign*term
sign = -sign
print(N, sum*4) |
# greg_mp.py: Gregory's series,
# multi-precision
from __future__ import print_function
from mpmath import *
mp.dps = 100
print("Precision: ", mp.dps)
N = 5000
sum = 0
sign = 1
for k in range(0,N):
term = 1/(mpf(2)*k + 1)
sum = sum + sign*term
sign = -sign
print(N, sum*4)
|
Notice that in the program at the right above, I only needed
to force one constant to be multi-precision, and then
mpmath forced each other variable and operation
to also be multi-precision. (There is no particular value in
relying on this, and it may make more sense to declare everything
multi-precision.)
Below, the blue digits are initial correct ones,
the red digits are incorrect,
and the green digits are
correct digits that come after at least one incorrect one.
| Gregory's Series,
up to 10 million terms, up to 100-digit accuracy. |
N= 10 3.041839618929402211135957
N= 100 3.131592903558552764307414238276920516403
N= 1000 3.140592653839792925963596502869395970451
N= 10000 3.1414926535900432384595183833748153787870136427443
N= 100000 3.1415826535897934884626433520295028937284193939649495759086359919592690
N= 1000000 3.1415916535897932387126433832791903841971703525001058155647883423571533203480491438917188683707422603
N= 10000000 3.1415925535897932384628933832795028810721693993752011334749445868976601562867023677686597593566434351
Exact:pi 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
1 2 3 4 5 6 7 8 9 0
1234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890 |
Items of Interest or for study:
- It was quick and easy to convert the ordinary Python program
to the arbitrary precision form.
- Notice the ordinary integer variables mixed in on the right:
N, sum, and k.
- This series converges very slowly, so that with 10000000
terms we only get 6 correct digits of pi to
the right of the decimal point.
However, amazingly, the green digits show a large number of correct
digits after incorrect ones. There are insanely too many for this to
be random chance, although any given random digit ought to be
correct with probability 1/10. Thus the isolated correct digits
above, and even pairs of correct digits (with probability
1/100), might be correct by chance.
Explanation for the above results:
These results suggest the existence of a sequence of
correction terms that would make the final sum much more accurate.
(See Gregory's Series
for further explanation.)
In fact, the phenomenon we are observing is an artifact of the particular
terms in Euler's famous formula for pi/4:
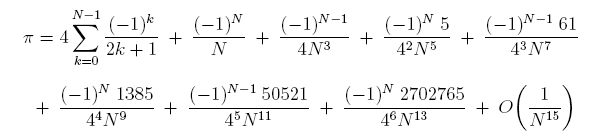One must first realize that the formula deals with so-called "real"
numbers. Inside the computer, one works with floating point
numbers, as a partial and finite representation of some real numbers.
In most computers the representation is in binary, in a special
hexadecimal form in Intel machines, and in actual binary in mpmath.
In some calculators, especially historically, the representation
has used decimal numbers. In spite of this, the strange results
in the table above, where there are more correct digits of pi
than one would expect, is a result of displaying certain results
in decimal form, and in adding up a number of terms that is
a power of 10. (These weird results were first noticed in 1988.)
In the formula above, the sum comes first.
Then the next term is (-1)N/N.
If N is a power of 10, say,
N = 10000, then that term will just
subtract 1 from the 4th place of the decimal expansion,
and make no other change. The table above shows that is exactly
what has happened.
The second term, with its pesky extra 4 in the denominator,
will end up subtracting the digits "025" (because of
the "one-fourth") from the decimal value, starting in the 12th digit,
and make no other change. Let's look at the numbers involved in detail
(this example is a bit weird, because adding in "25" changes
the previous 2 digits because of carries):
Exact:pi 3.1415926535897932384626433832795028841971693993751
- 0.000100000000000000000000000000000000000000000000
= 3.1414926535897932384626433832795028841971693993751
+ 0.0000000000002500000000000000000000000000000000
= 3.1414926535900432384626433832795028841971693993751
If you look at the earlier table, you can see that on each line, the
first red digit is the result of subtracting a "1" from pi at the
proper place, and the next pair of red digits results from adding
"25" at the proper place.
With higher powers of 4 and with a numerator not equal to 1,
each new term makes successively larger contributions to the total,
though starting further and further out in the decimal expansion
and always ending in non-terminating 0's.
I emphasize that these results depend on using decimal (base 10) representations,
and on a power of ten as the number of terms added up.
One gets similar and even more impressive results for 5 followed
by a power of ten, as shown in the table below, and less impressive
such results for, say, 2, 4, or 8 followed by a power of ten,
and for other numbers of terms.
Gregory's Series, more sums:
Here I'm showing additional sums of Gregory's series,
computed with up to 250-digit accuracy and up to 10 billion terms.
I'm also including those with a five followed by a power of ten.
I have no intuition about why starting with a five gives better results.
This single calculation took about 25 days on my slow and old
PC at home.
|
