CS 3721
Programming Languages  
Fall 2013
 Recitation 2. REs & ε-moves 
Week 2: Sep 4 - 6

Note: Dates below changed on 10 Sep 2013 (2 and 3 days later).
Submit following directions at: submissions and rules at: rules. Deadlines are:
  • 2013-09-13  23:59:59 (that's Fri, 13 Sep 2013, 11:59:59 pm) for full credit.
  • 2013-09-16  23:59:59 (that's Mon, 16 Sep 2013, 11:59:59 pm) for 75% credit.

1. Regular Expressions Read the page Regular Expressions. You need to understand the three operators used in regular expressions: their meaning, use, and precedence. You will see a number of examples.

  1. Give a regular expression that describes any string made of as, bs, and cs, with either at least one a somewhere or at least 2 bs somewhere. (You should only use the notation in the link above, and not other fancy notation. For example, no + operator.)

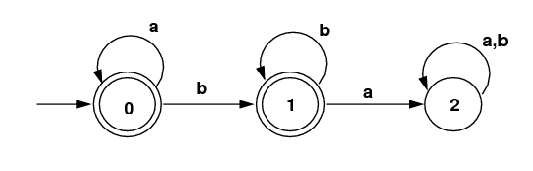
  2. Consider the FA below. Is it an NFA or a DFA? Give a regular expression representing this FA. (Be careful to notice which states are final states.)

    .

2. ε-moves: ε-closure algorithm Read the page NFAs with ε-moves. You need to understand the ε-closure algorithm.

Consider the NFA in Example 1 of the page RE −−> NFA that describes how to translate any regular expression into an NFA that accepts the same language. In this case the regular expressions is /.*(ab|aac)/, but here we're only interested in the first two steps of the subset algorithm applied by hand to this NFA, as part of the process of converting this NFA into a DFA, by hand. Later we'll talk much more about the whole process.

  1. Notice that the start state of the NFA is 2. The start state for the corresponding DFA won't be {2}, but will be ε-closure({2}). You are to apply the ε-closure algorithm to {2} step-by-step, showing at each stage states pushed on the stack and showing states as they are colored black. (The collection of all black states is the ε-closure.)

  2. Next, assume that the first input character is an "a". You are to calculate the result of following an arrow labeled with "a" or with "." to another state and making a set of these states. [Answer: {1,5,9}.]

  3. Finally, calculate ε-closure({1,5,9}) and show the calculation step-by-step as in the first item above.

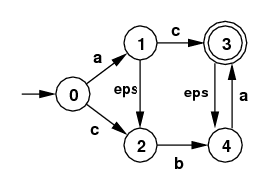
3. ε-moves: Subset Algorithm Read the page NFAs with ε-moves. You should understand how the subset algorithm is extended to NFAs with ε-moves.

  1. Use the extended subset algorithm to find the DFA that corresponds to the following NFA:

  2. Suppose you want to handle the regular expression: /ab(ab)*/. The figure below gives this converted to an NFA with ε-moves. (Here "@" is what I use for ε in programs (ε = the empty string). This isn't the only NFA that will work, but this is the one you must work with. Below, the transition from state 7 to state 10 should be labeled with @.)

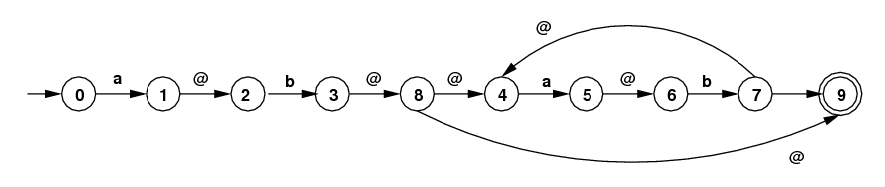
    1. Carry out the extended subset algorithm on this NFA to get a DFA that accepts the same language. [Your answer should have 6 states including the empty set as an error state.]

    2. This DFA is not optimal: it doesn't have the minimal number of states. But it can be converted to that optimal DFA by identifying two of its states. Say which two need to be identified.

Revision date: 2013-09-05. (Please use ISO 8601, the International Standard.)