CS 3723
 Programming Languages 
  NFAs with ε Moves  

Introduction. You should first study the web pages:

NFAs with ε moves: Here one allows transitions labeled with ε, the empty string. This means that you can follow such an arrow without consuming any input symbols. The NFA on the left shows how useful epsilon moves are in recognizing regular expressions with the example a*b*c*: which is "zero of more as, followed by zero or more bs, followed by zero of more cs". (The diagram uses "eps" for ε.)

On the right is a DFA that recognizes the same language. Notice some new things about this DFA: three states are terminal ones, including the start state. There is an "error" state, with label err, and it is not terminal. If you transition to that state, you can't get out and you can't accept. This state could also have been labeled with the symbol for the empty set: Ø

A refinement or expansion of the Subset Algorithm shows how to construct this DFA.


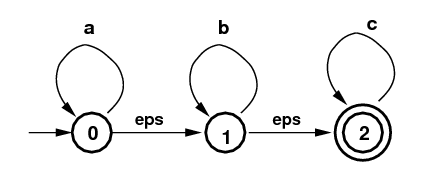NFA for a*b*c*

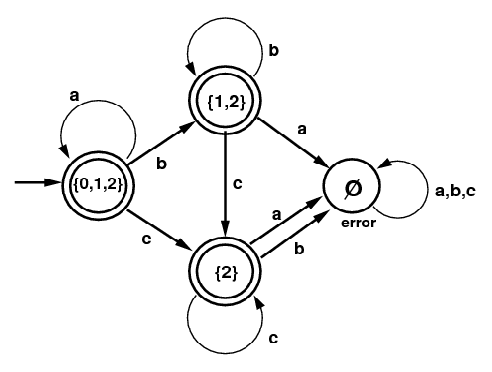DFA for a*b*c*
Subset Algorithm (Tables)
DFA, a*b*c*
Statesabc
  {0,1,2} (start,term) {0,1,2}{1,2}{2}
  {1,2} (term) Ø{1,2}{2}
  {2} (term) ØØ{2}
  Ø ØØØ

[See Computer Simulation of the NFA and DFA above.]

ε-closure: The key to constructing a DFA from an NFA with ε-moves is the ε-closure algorithm. The starts with a set of states and find all additional states that can be reached from the given states using ε-moves.

Algorithm: ε-closure
Input: an NFA with ε-moves N, a set P of states.
Output: ε-closure(P), which is P along with all states
   reachable from P by a sequence of ε-moves.
Method: use stack S to carry out a depth-first search
// black means in ε-closure(P)
color all states white
color all states of P black
push all states of P onto S
while (S not empty) {
   u = pop(S)
   for (each edge (u,v) labeled ε) {
      if (v has color white) {
         color v black
         push v
      }
   }
}
ε-closure(P) = black states
   
The subset algorithm for an NFA with ε-moves is the same as the one for ordinary NFAs, except that each time a subset is constructed, it must have the ε-closure algorithm (at the left) applied to it.

In the above case, the start state of the NFA is 0, so the start state of the DFA is not {0} but ε-closure({0}) = {0,1,2}.

Transitions on b from 0, 1, or 2 only go to 1. Then ε-closure({1}) = {1,2}..

There are no transitions on a from 1 or 2, so the set in this case is Ø, the empty set. The empty set is a subset that serves as an error state.

Revision date: 2013-06-09. (Please use ISO 8601, the International Standard.)