CS 3723
 Programming Languages 
  RE −−> NFA  

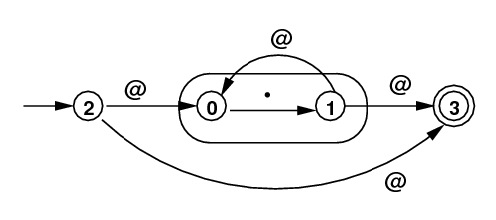
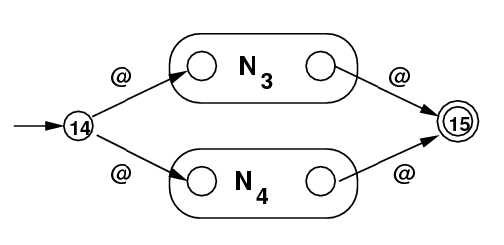
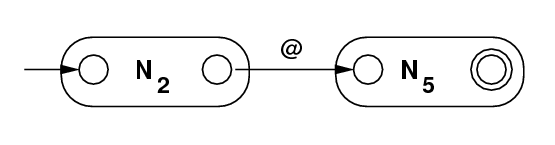
Regular Expression −−> NFA with ε-moves: Given an arbitrary regular expression R, it describes a language, that is, a set of strings of symbols over some alphabet. From R, we want to create an NFA with ε-moves called N so that N accepts any string described by R and rejects any other string. Then we would implement N with a program. The result a regular expression recognizer.

First we would use syntax techniques that will be presented later in this course to break R up into a sequence of elementary steps, each one using a single operator. Then we handle the operators one-at-a-time to translate to N. The table below shows how this can be done, with each component regular expression on the left and the corresponding NFA on the right.

Regular
Expression		 NFA with ε-moves
Constructed

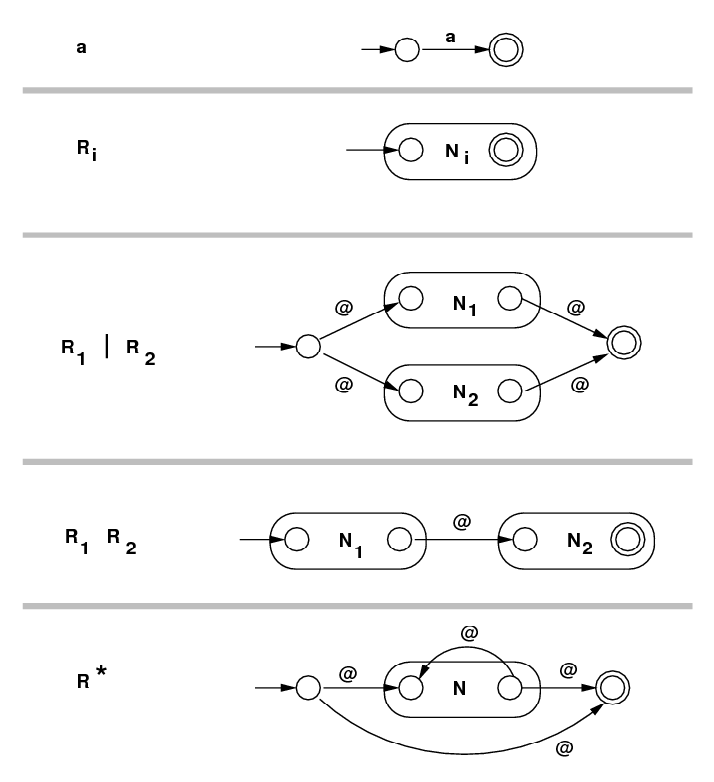
Example 1: We'll use a slash at the start and end of our regular expressions. Suppose
    R = /.*(ab|aac)/
Here is a sequence of regular expressions, culminating in R:

Regular ExpressionNFA
Name		 NFA with ε-moves
 R1 = .
 (matches any
  symbol)		  N1 
 R2 = R1*
 (star operator)		  N2 
 R3 = ab
 (concatenation)		  N3 
 R4 = aac
 (concatenation
  twice)		  N4 
Regular
Expression		NFA
Name		 NFA with ε-moves
 R5 = R3 | R4 
 (or operator)		  N5 
 R = R2R5
 (concatenation)		  N 

Programming Example 1:

  • Regular Expression:   /.*(ab|aac)/
  • RPN Form or Regular Expression:   .*ab+aa+c+|+$
  • Input String to Match:   cabcaaacabac$
  • Corresponding Ruby Program:   abaac.rb

Input
Processed		 NFA
(so far)		 NFA
(graph representation)		Controlling
Stack
. 
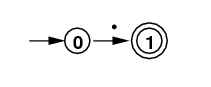 0 --> [., 1]
 1
 
[0, 1](top)
.* 
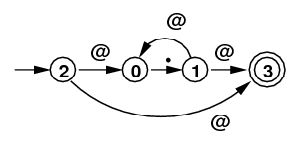 0 --> [., 1]
 1 --> [@, 0] --> [@, 3]
 2 --> [@, 3] --> [@, 0]
 3
 
[2, 3](top)
.*ab+ 
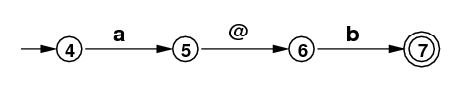 4 --> [a, 5]
 5 --> [@, 6]
 6 --> [b, 7]
 7
 
[4, 7](top)
[2, 3]
.*ab+aa+c+
    (2 steps)		 
 8 --> [a, 9]
 9 --> [@,10]
10 --> [a,11]
11 --> [@,12]
12 --> [c,13]
13
 
[8,13](top)
[4, 7]
[2, 3]
.*ab+aa+c+|+
    (2 steps)
 
 0 --> [., 1]
 1 --> [@, 0] --> [@, 3]
 2 --> [@, 3] --> [@, 0]
 3 --> [@,14]
 4 --> [a, 5]
 5 --> [@, 6]
 6 --> [b, 7]
 7 --> [@,15]
 8 --> [a, 9]
 9 --> [@,10]
10 --> [a,11]
11 --> [@,12]
12 --> [c,13]
13 --> [@,15]
14 --> [@, 8] --> [@, 4]
15 --> 
[2,15](top)

Simulating the NFA in Example 1:

NFA
(graph representation)		 Simulation
Trace
Reg. Expr: /.*(ab|aac)/
RPN Form: .*ab+aa+c+|+$
The NFA as a graph:
 0 --> [., 1]
 1 --> [@, 0] --> [@, 3]
 2 --> [@, 3] --> [@, 0]
 3 --> [@,14]
 4 --> [a, 5]
 5 --> [@, 6]
 6 --> [b, 7]
 7 --> [@,15]
 8 --> [a, 9]
 9 --> [@,10]
10 --> [a,11]
11 --> [@,12]
12 --> [c,13]
13 --> [@,15]
14 --> [@, 8] --> [@, 4]
15 --> 

Input string to match:
cabcaaacabac$
Successive sets of states:
 |                     1 1 1 1 1 1 
 | 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 
 | - - - - - - - - - - - - - - - - 
 : 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 s
 : 1 0 1 1 1 0 0 0 1 0 0 0 0 0 1 0 s
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
b: 1 1 0 1 1 0 0 1 1 0 0 0 0 0 1 1 t
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0  
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 1 1 1 t
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
b: 1 1 0 1 1 0 0 1 1 0 0 0 0 0 1 1 t
a: 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0  
c: 1 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0

Example 2:
  • Regular Expression:   /.*(ab|ac)(ab|ac)*d/
  • RPN Form or Regular Expression:   .*ab+ac+|+ab+ac+|*+d+$
  • Input String to Match:   aabacacdccacabddaadcad$

NFA
(graph representation)		 Simulation
Trace
Reg. Expr:
/.*(ab|ac)(ab|ac)*d/
RPN Form:
.*ab+ac+|+ab+ac+|*+d+$
The NFA as a graph:
 0 --> [., 1]
 1 --> [@, 0] --> [@, 3]
 2 --> [@, 3] --> [@, 0]
 3 --> [@,12]
 4 --> [a, 5]
 5 --> [@, 6]
 6 --> [b, 7]
 7 --> [@,13]
 8 --> [a, 9]
 9 --> [@,10]
10 --> [c,11]
11 --> [@,13]
12 --> [@, 8] --> [@, 4]
13 --> [@,24]
14 --> [a,15]
15 --> [@,16]
16 --> [b,17]
17 --> [@,23]
18 --> [a,19]
19 --> [@,20]
20 --> [c,21]
21 --> [@,23]
22 --> [@,18] --> [@,14]
23 --> [@,22] --> [@,25]
24 --> [@,25] --> [@,22]
25 --> [@,26]
26 --> [d,27]
27 --> 

Input string to match: aabacacdccacabddaadcad$
Successive sets of states:
 |                     1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 
 | 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 
 | - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
 : 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 s
 : 1 0 1 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 s
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
b: 1 1 0 1 1 0 0 1 1 0 0 0 1 1 1 0 0 0 1 0 0 0 1 0 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0  
c: 1 1 0 1 1 0 0 0 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 1 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0  
c: 1 1 0 1 1 0 0 0 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 1 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 t
c: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
c: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
c: 1 1 0 1 1 0 0 0 1 0 0 1 1 1 1 0 0 0 1 0 0 0 1 0 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0  
b: 1 1 0 1 1 0 0 1 1 0 0 0 1 1 1 0 0 1 1 0 0 0 1 1 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 t
d: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
d: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
c: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0  
d: 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Example 3:
  • Regular Expression:   /.*(ab)*c/
  • RPN Form or Regular Expression:   .*ab+*+c+$
  • Input String to Match:   dddabababcdddababcddd$
  • Corresponding Ruby Program:   ab.rb

NFA
(graph representation)		 Simulation
Trace
Reg. Expr:
/.*(ab)*c/
RPN Form:
.*ab+*+c+$
The NFA as a graph:
   0 --> [., 1]
   1 --> [@, 0] --> [@, 3]
s  2 --> [@, 3] --> [@, 0]
   3 --> [@, 8]
   4 --> [a, 5]
   5 --> [@, 6]
   6 --> [b, 7]
   7 --> [@, 4] --> [@, 9]
   8 --> [@, 9] --> [@, 4]
   9 --> [@,10]
  10 --> [c,11]
t 11 --> 

Input string to match:
dddabababcdddababcddd$
Successive sets of states:
 |                     1 1 
 | 0 1 2 3 4 5 6 7 8 9 0 1 
 | - - - - - - - - - - - - 
 : 0 0 1 0 0 0 0 0 0 0 0 0  s
 : 1 0 1 1 1 0 0 0 1 1 1 0  s
d: 1 1 0 1 1 0 0 0 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0  
b: 1 1 0 1 1 0 0 1 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0  
b: 1 1 0 1 1 0 0 1 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0  
b: 1 1 0 1 1 0 0 1 1 1 1 0  
c: 1 1 0 1 1 0 0 0 1 1 1 1  t
d: 1 1 0 1 1 0 0 0 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0  
b: 1 1 0 1 1 0 0 1 1 1 1 0  
a: 1 1 0 1 1 1 1 0 1 1 1 0  
b: 1 1 0 1 1 0 0 1 1 1 1 0  
c: 1 1 0 1 1 0 0 0 1 1 1 1  t
d: 1 1 0 1 1 0 0 0 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 1 1 0  
d: 1 1 0 1 1 0 0 0 1 1 1 0

Example 1 Without ε-moves: Here is the final NFA with ε-moves (called N above) written in a simple way as an NFA without ε-moves. It will be a recitation exercise to transform this into a DFA that accepts the same language.

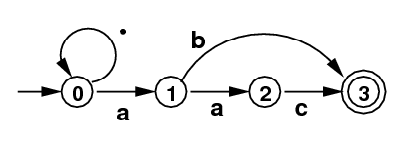
Revision date: 2013-09-07. (Please use ISO 8601, the International Standard.)