CS 3723: Finite Automata, Subset Algorithm

	CS 3723 Programming Languages
Finite Automata: Subset Algorithm

Introduction: This page is a continuation of the page Finite Automata, so you should read that first. On this page we describe an algorithm that converts an arbitrary NFA into a DFA that accepts the same language as the NFA.

Example 1: Below on the left is the NFA defined by the regular expression (a|b)*abb. As a first step in this example, let's consider the string a b a a b b a b b b presented as input to this NFA. Already with the initial a there is a problem: Should we say in State 0, or move to State 1? Instead let's do the following: keep track at each stage of all the possible states we might be in:

All Possible States

Next
Input Set of States

- {0} (start)

a {0,1}

b {0,2}

a {0,1}

a {0,1}

b {0,2}

b {0,3} (term)

a {0,1}

b {0,2}

b {0,3} (term)

b {0}

b {0}

Now suppose we have a new FA with each of the various sets if states at the left as the new "states" of this FA. The table at the left also shows transitions between the new states.
New states:
{0}, {0,1}, {0,2}, {0,3}.
New Transitions:
{0} −−a−−> {0,1} {0,1} −−b−−> {0,2} {0,2} −−a−−> {0,1} {0,1} −−a−−> {0,1} {0,2} −−b−−> {0,3} {0,3} −−b−−> {0} {0} −−b−−> {0} {0,3} −−a−−> {0,1}
Now draw all these together in a diagram, and you get the illustration on the right below. Notice that there are 16 subsets of the set {0,1,2,3} of all states, but we are only using 4 of them. (Ignore the others.)
We've created a DFA that processes characters and keeps track at each stage of all the possible states of the old NFA that you might end up in.

The state {0,3} contains a terminal state of the original NFA, so it is a terminal state of the new DFA, since it's possible to be in a terminal state at that point.

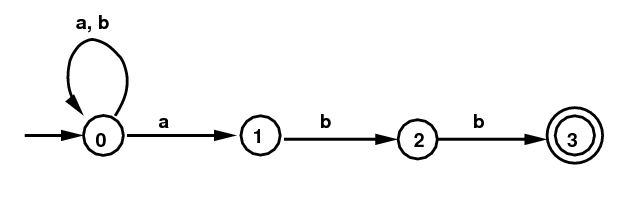NFA for (a|b)*abb

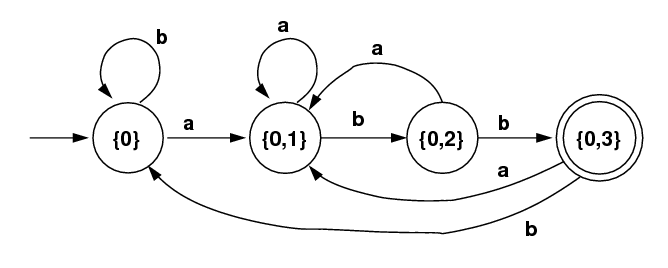DFA for (a|b)*abb

Subset Algorithm (Tables)

NFA, (a\|b)*abb
State	a	b
0 (start)	0,1	0
1	−	2
2	−	3
3 (term)	−	−

DFA, (a\|b)*abb
States	a	b
{0} (start)	{0,1}	{0}
{0,1}	{0,1}	{0,2}
{0,2}	{0,1}	{0,3}
{0,3} (term)	{0,1}	{0}

[See All States for the same example of the subset algorithm showing all possible states and all transitions.]

Example 2: Below on the left is another example: the NFA defined by the regular expression (a|b)*(aa|bb)(a|b)*. Let's work out one transition in this example. Suppose the DFA on the right is in state {0,1}. Suppose the next input symbol is a b. Then if the original NFA was in state 0, it could transition to either 0 or to 1. If it was in state 1, there is no transition. So the new transition on b in the new DFA goes from state {0,1} to state {0,2}.

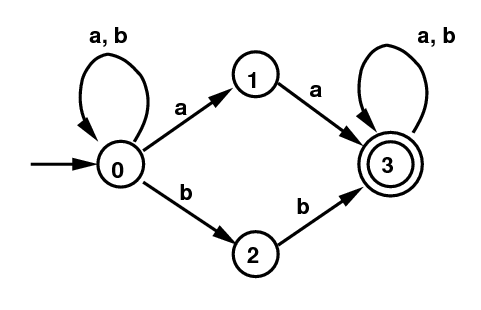NFA for (a|b)*(aa|bb)(a|b)*

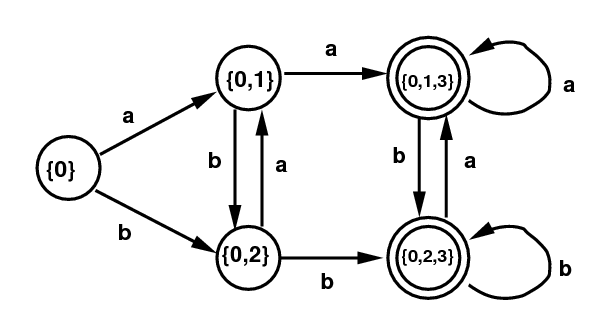DFA for (a|b)*(aa|bb)(a|b)*

Again we represent the NFA using a table at the left. This makes it easier to see how the corresponding DFA at the right is constructed. Assuming 0 is the NFA start state, {0} will be the DFA start state. After processing each line of the DFA table, you add any new subset states that came into being as new lines at the right. This process has to terminate because there are only finitely many subsets. At each stage, you take each element of the DFA subset at the right, say it is {0,1}. Then take the union of the corresponding states in the table at the left. So the result of symbol a from {0,1} will be the set containing 0 and 1, along with 3, or {0,1,3}. Each entry is handled this way.

Subset Algorithm (Tables)

NFA, (a\|b)(aa\|bb)(a\|b)
State	a	b
0 (start)	0,1	0,2
1	3	−
2	−	3
3 (term)	3	3

DFA, (a\|b)(aa\|bb)(a\|b)
States	a	b
{0} (start)	{0,1}	{0,2}
{0,1}	{0,1,3}	{0,2}
{0,2}	{0,1}	{0,2,3}
{0,1,3} (term)	{0,1,3}	{0,2,3}
{0,2,3} (term)	{0,1,3}	{0,2,3}

Formal Algorithm: In studying this algorithm, we will keep referring to the specific Example 2 above.

Let N be an NFA. This means we have a set Σ of symbols, a list A of states, which are just non-negative integers, a start state, which we assume is 0, and a list B of terminal states, which is a sublist of A. (Possibly B = A. B must be non-empty. Possibly 0 is in B.)

N also has a transition function T. For each state x, and for each symbol u, T(x,u) is a list of states of N, possibly an empty list. Starting with state x, and given the symbol u, this list consists of the states that can be transitioned to, from x given symbol u. Above on the left is a definition of T for Example 2.

We will construct a DFA D that accepts the same language as N. D will have the same set Σ of symbols as N. The states of D will be sets of states of N, including possibly the empty set. The start state of D will be {0}, assuming 0 is the start state of N.

The algorithm below will construct a list A' of states of D, where each state is a set of the states of N. We will use a queue Q holding states of D, as they are produced by the algorithm. The algorithm will also define the transition function T' of D, and the list B' of terminal states of N.

Algorithm: Given N as above, construct D.

Add {0} to A'. // add start state of D to list of states of D
Insert {0} into Q. // put state state of D into queue
while (Q is not empty) {
   R = remove(Q). // R = state of D = set of states of N
   S = Ø. // S = state of D to be constructed, initially empty
   for (each symbol u) { // define T'(R,u) for each symbol u
      for (each x in R) { // x = integer, a state of N
         S = {T(x,u)} union S.
      }
      if (S not on the list A') {
         Add S to A'. // new state S in list A'
         Insert S into Q. // new state S in list queue Q
      }
      T'(R,u) = S.
   }
}
B' = all states of A' containing a state of B.

State Minimization: It turns out that the DFA constructed by the subset algorithm is not necessarily as simple as possible. That's the case for the DFA on the right above. It is equivalent to the DFA below, obtained by identifying the two terminal states. For simplicity I also renamed the states. There exists a state minimizing algorithm, which I won't present here. Any NFA has a unique equivalent DFA with a minimum number of states. (Well, unique up to renaming things.)

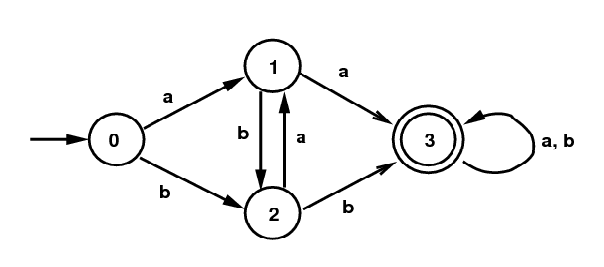
Minimal DFA for (a|b)*(aa|bb)(a|b)*
With States Renamed

Example 3: This time start with a slightly different NFA defined by the same regular expression from Example 2: (a|b)*(aa|bb)(a|b)*. The corresponding DFA, given by the subset algorithm, is much more complicated. The final minimal DFA is the same as the last DFA in the previous section (just above this sentence). Again the minimal DFA is obtained by identifying all 6 of the terminal states.

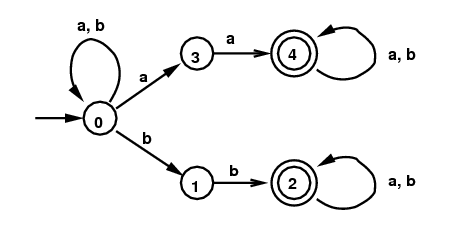NFA for (a|b)*(aa|bb)(a|b)*

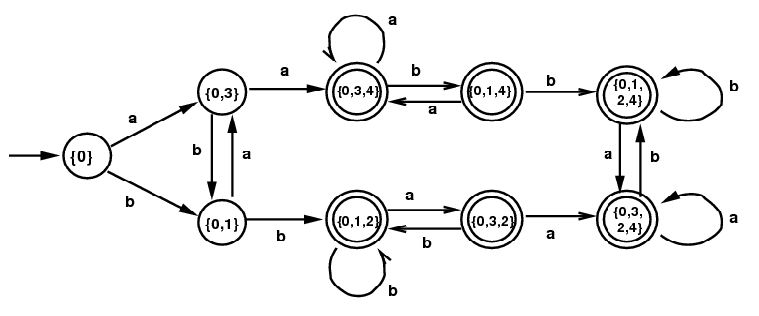DFA for (a|b)*(aa|bb)(a|b)*

Subset Algorithm (Tables)

NFA, (a\|b)(aa\|bb)(a\|b)
State	a	b
0 (start)	0,3	0,1
1	−	2
2 (term)	2	2
3	4	−
4 (term)	4	4

DFA, (a\|b)(aa\|bb)(a\|b)
States	a	b
{0} (start)	{0,3}	{0,1}
{0,3}	{0,3,4}	{0,1}
{0,1}	{0,3}	{0,1,2}
{0,3,4} (term)	{0,3,4}	{0,1,4}
{0,1,2} (term)	{0,2,3}	{0,1,2}
{0,1,4} (term)	{0,3,4}	{0,1,2,4}
{0,2,3} (term)	{0,2,3,4}	{0,1,2}
{0,1,2,4} (term)	{0,2,3,4}	{0,1,2,4}
{0,2,3,4} (term)	{0,2,3,4}	{0,1,2,4}

Examples 4: Here is a different NFA, obtained from the regular expression (a|b)*a(a|b)(a|b). The DFA on the right below comes from the same subset algorithm. In this case it is already the minimum state DFA. (The diagram on the right gives the subsets without commas or curly brackets.)

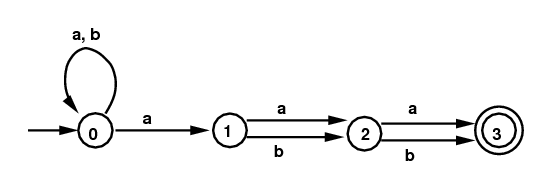NFA for *(a\|b)a(a\|b)(a\|b)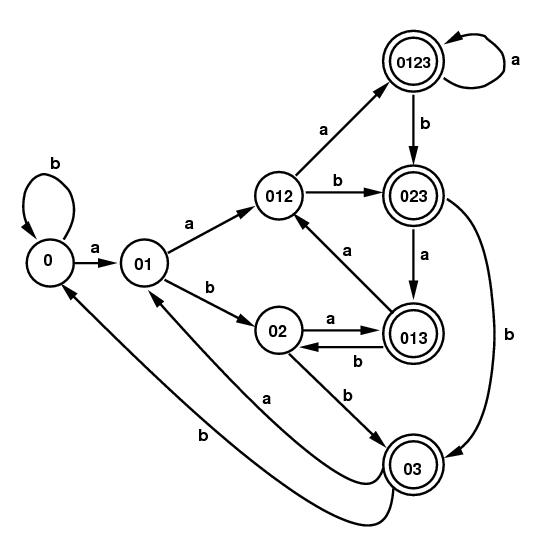**	DFA for *(a\|b)a(a\|b)(a\|b)**

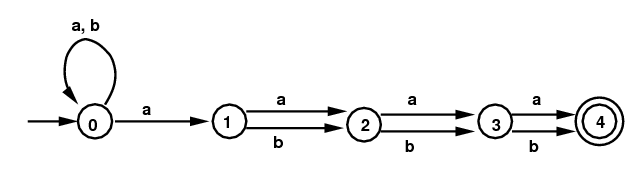Next, start with a similar NFA with 1 additional state. In this case the DFA has twice as many states, and it again is minimal.

NFA for *(a\|b)a(a\|b)(a\|b)(a\|b)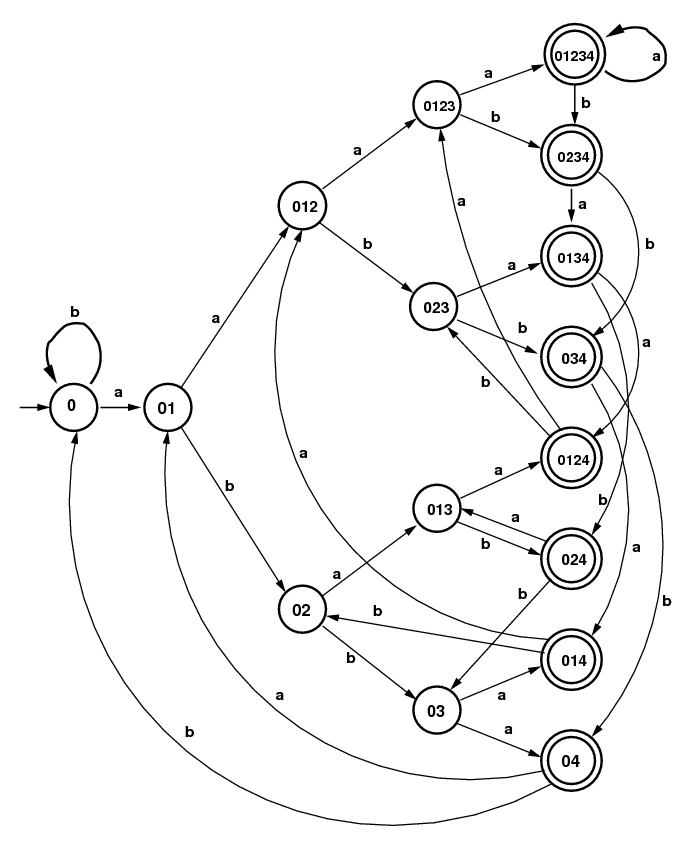**	DFA for (a\|b)a(a\|b)(a\|b)(a\|b) Note: Label on arrow from (03)* to ((04)) should be "b".

In general, suppose one starts with a regular expression built from (a|b)*a followed by n copies of (a|b). This NFA has states 0, 1, ... , n, and the corresponding minimal DFA has 2ⁿ states. In fact the subsets needed by this DFA are exactly the 2ⁿ subsets of the set {0,1,...,n} that contain 0.

Revision date: 2014-03-17. (Please use ISO 8601, the International Standard.)