CS 3723
 Programming Languages 
  Finite Automata  

Languages: Start with a finite set of symbols called an alphabet, such as {0, 1}, or {a, b, c, d}, or the set of all Ascii characters. A finite string of these symbols is called a sentence. A language is a set of sentences. Thus a language is just some set of strings of symbols. For example, the set E of all strings of 0s and 1s with an even number of 1s is a language. (E = even parity bit-strings.)

Notice that everything is finite except for the language, where in the interesting cases there are infinitely many sentences, as with the example above. We want to give finite descriptions of languages, including infinite languages. Consider another example: the set L of all strings of as and bs that end with "abb". The previous (English) sentence is an informal finite description. It would (of course) be impossible to list the elements of this language, but we could start: L = {abb, aabb, babb, aaabb, ababb, baabb, bbabb, aaaabb, aababb, ...}. The language L can be described or generated by the regular expression (a|b)*abb.

If Σ denotes the alphabet, then (using regular expression notation), Σ* denotes the set of all finite strings of symbols from the alphabet. This includes the empty string "", which is denoted by the lower-case Greek letter epsilon = ε. Thus any subset of Σ* is a language. (In particular, the sets Σ* of all finite strings, and the empty set Ø of no strings are languages.)

Finite Automata (FA) (singular: "finite automaton"): These are also called Finite State Machines (FSM). [These are defined informally below to make the concepts easier. It is possible to give a formal, precise, and mathematical definition of FSMs.]

An FA consists of:

  • a finite set of states, each represented by a circle, with the name of the state inside. We will usually use successive integers starting with 0 as names, but the name can be anything.

  • a finite set of transitions from state to state, each represented by an arrow going from state to state. A transition can go from a state to itself. The transition arrows are labeled with one or more symbols. The transition arrows are followed as input symbols for the alphabet are processed. The input symbol must match the label on the transition.

  • One state (never more than one) must be designated the start state or initial state. This state is identified by an arrow with no start, but ending at the state.

  • Any number of states (but at least one) must be designated the terminal states or final states or accepting states. These are identified using a double circle. The start state can also be a terminal state.

Here is a diagram of an FA:


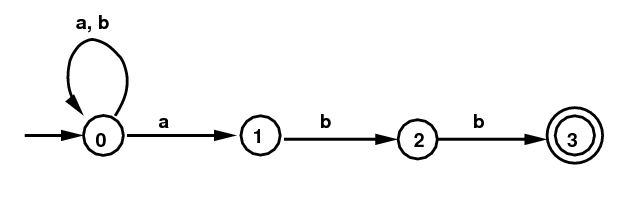
NFA for the RE (a|b)*abb

Here the alphabet is {a, b} and the set of states is {0, 1, 2, 3}. The start state is 0, denoted by an initial arrow. There is only one terminal state, 3, denoted by a double circle around it.

  • NFAs. The particular FA above is called a Non-Deterministic Finite Automaton (NFA).

    This NFA is said to recognize the language L above (the one described by the RE (a|b)*abb.)

    In order to recognize strings from L with the NFA above, we process an input string character-at-a-time, starting with the 0th character, and starting at the start state 0. As you read each character, it is processed by following an arrow labeled with that character. If we can manage (somehow, in any way) to end up in the terminal state 3 just as we finish all the characters in the string, we accept the string as belonging to L. Otherwise we reject the string.

    This automaton is called non-deterministic because there is a case (there must be at least one, or else it would be called a DFA; see below) with two or more possible choices for the arrow to take.

    Suppose we are processing the symbol a in the string "abaabbaabb". How do we know when to leave state 0 and finish the string? (We could decide with a look-ahead buffer, but we want a simpler solution.)

  • DFAs Given an NFA, it is always possible to create what is called a Deterministic Finite Automaton (DFA) that recognizes the same language. For the language L above, here is the corresponding DFA:


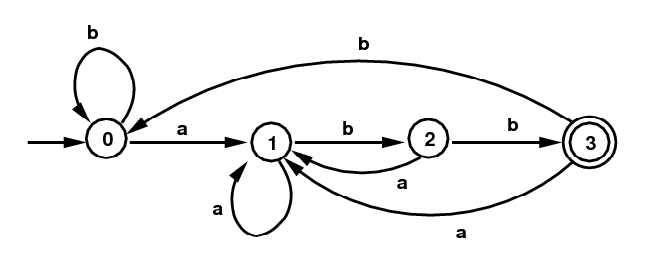
    DFA for (a|b)*abb

    This automaton is called deterministic because in each case there is exactly one choice for which arrow to follow. The process is uniquely determined. If you end up in the terminal state 3, and have reached the end of the string, then you accept the input string as belonging to L and otherwise you reject it.

    We'll also call an automaton a DFA in case there is at most one choice for which arrow to follow. In case there is an input symbol and no choice of arrow to follow, this is considered an error. We can add an extra error state and add a transition to the error state in case there was no choice.

There is a clever algorithm for constructing a DFA that recognizes the same language as a given NFA (the "subset algorithm") which we will cover in the course. These two examples above of an NFA and corresponding DFA both have the same numbered states and look very similar. This similarity is an artifact of such simple examples. In general the corresponding DFA will be much more complex than the original NFA. In the worst case it will be exponentially larger.

FAs = REs: Finite automata are exactly equivalent to regular expressions. If a given FA recognizes a certain language, there always is an equivalent RE that describes exactly the same language. Similarly, given an RE that describes a given language, there is always an FA that recognizes the same language.

These languages are much simpler than the languages described by CF grammars, which we will study in a few weeks. CF grammars include REs and FAs as special cases.

(Revision date: 2014-06-20. (Please use ISO 8601, the International Standard.)