| |
 |
CS 3723
Programming Languages |
Subset Algorithm:
Showing All States |
Introduction:
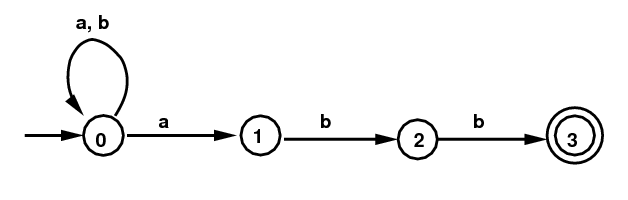
On this page we're doing the Subset Algorithm for the simple
NFA given by /(a|b)*abb/, except that we show the
transitions from all possible states, not just the ones
reachable from the start state of the NFA. With 4 states
in the NFA, there are 24 = 16 possible states
to use for the DFA. The black parts of the diagram on the right
below give the DFA, while the red parts give additional states
that are not reachable, and therefore are of no interest.
The number of possible states for a DFA grows exponentially,
but one seldom needs an exponential number. This is why
it is important to ignore the unreachable states.
|
|
| Subset Algorithm
(Tables) |
|---|
| NFA,
(a|b)*abb |
|---|
| State | a | b |
|---|
| 0 (start) | 0,1 | 0 |
|---|
| 1 | − | 2 |
|---|
| 2 | − | 3 |
|---|
| 3 (term) | − | − |
|---|
| |
| DFA,
(a|b)*abb |
|---|
| States | a | b |
|---|
| {0} (start) |
{0,1} | {0} |
|---|
| {0,1} |
{0,1} | {0,2} |
|---|
| {0,2} |
{0,1} | {0,3} |
|---|
| {0,3} (term) |
{0,1} | {0} |
|---|
|
| {0,1,2} |
{0,1} | {0,2,3} |
|---|
| {0,2,3} (term) |
{0,1} | {0,3} |
|---|
| {0,1,3} (term) |
{0,1} | {0,2} |
|---|
| {0,1,2,3} (term) |
{0,1} | {0,2,3} |
|---|
|
| {1} |
Ø | {2} |
|---|
| {2} |
Ø | {3} |
|---|
| {3} (term) |
Ø | Ø |
|---|
| {1,2} |
Ø | {2,3} |
|---|
| {2,3} (term) |
Ø | {3} |
|---|
| {1,3} (term) |
Ø | {2} |
|---|
| {1,2,3} (term) |
Ø | {2,3} |
|---|
| Ø |
Ø | Ø |
|---|
|
|
(Revision date: 2014-08-28.
Please use ISO
8601, the International Standard.)
|
