(Textbook. Click for information.)

CS 3343/3341  Analysis of Algorithms  Spring 2012  Recitation 11  Dijkstra and Log2     Week 11: Apr 10-Apr 12  Due (on time): 2012-04-16  23:59:59  Due (late):        2012-04-20  23:59:59

Recitation 11 should be submitted following directions at: submissions with deadlines 2012-04-16  23:59:59 (that's Monday, 16 April 2012, 11:59:59 pm) for full credit. 2012-04-20  23:59:59 (that's Friday, 20 April 2012, 11:59:59 pm) for 75% credit.

Note: As of < Fri Apr 13 19:51:31 CDT 2012 > I put up the submission program for this recitation and tested it.

---

1. This problem asks you to write a program that will find log₂x, where x is an arbitrary positive double. For full credit, your program must not include any transcendental functions. You must include at least three runs: one inside the normalization interval, one much smaller than the lower number of this interval, and one much larger than the upper number of this interval. (The latter two runs are to test the normalization.)

   The method used in based on methods in the web page 6 Newton's Method 1. Detailed specifications of this problem are at Rec 11, Problem 1.

   ---

2. For this problem, you are to implement Dijkstra's algorithm, found on page 658 of your text. (This algorithm was covered in the recitation section.)
   

   The function Initialize-Single_source(G,s) is defined on page 648, and sets the d field of each vertex to +infinity and the π field to NIL. The the d field for s is set to 0 (overwriting the previous value). The function Relax(u,v,w) is found on page 649, and is defined by:

   Relax(u, v, w)   if v.d > u.d + w(u, v)       v.d = u.d + w(u, v)       v.π = u

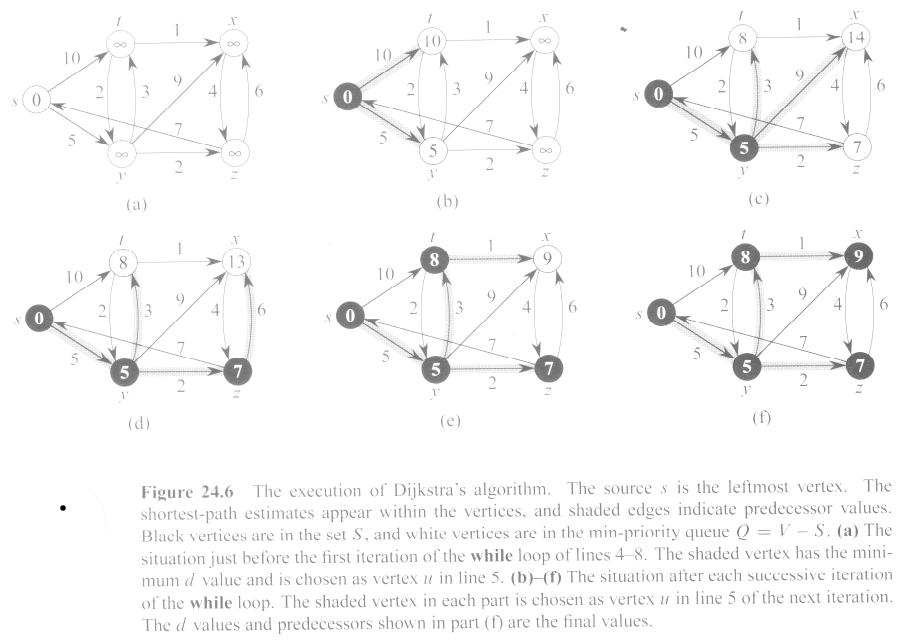
   The set S of vertices on lines 2 and 6 is only used for the correctness proof, so it need not be implemented. The function puts all vertices into a minimum priority queue, and so each Extract-Min returns the vertex with the smallest remaining d value. (The priority queues we got from heaps were max priority queues.) You may use any kind of min-priority queue that you can find or put together. Probably the simplest solution is to fake such a queue, meaning to store the list of values and repeatedly search for the vertex with the current smallest value of the field d, returning and deleting it, without worrying about performance.

   More about the queue: Beware! The d fields change from step to step during execution, so the queue will need the latest d values to return the proper vertex. In writing this code, I did not try to use a true priority queue based on heaps, but instead created a simple low-performance queue. Nevertheless, I found this part the most confusing, since the priority of removal is based on the latest values of the d fields. I did this algorithm a long time ago and thought it was easy; you could use an extra field (color black or white) on each vertex to keep track of those vertices not yet processed (color=white). Then repeatedly go down the list looking for the white vertex with smallest d value.

   You must carry out at least two runs of your program that implements Dijkstra's algorithm, including both RUN A, and RUN B below:

   ---

   RUN A. Use the example in your text (Figure 24.6 on page 659, and shown below). Notice that this is a directed graph, so you enter each vertex only once in the proper direction. Your text's vertices are: s, t, x, y, z. I labeled these 0, 1, 2, 3, 4 in that order. Here is a file containing the edges and weight descriptions: fig24.6.txt with an initial 5 for the number of vertices.

---

RUN B. For the second run, use our standard example: the capitals and distances between them. We regard this as a directed graph with each edge going in both directions. You should use a source vertex of your choice.