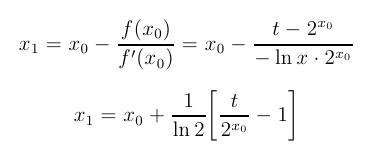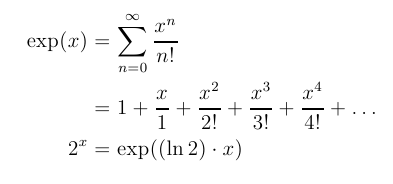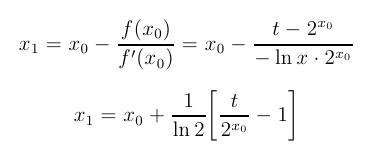
CS3343/3341 Analysis of Algorithms Spring 2012 |
Recitation 11
Problem 1 Calculating log2x |
public double approx(double x) {
double a0 = -2.1718276908;
double a1 = 3.0858266589;
double a2 = -1.0780415294;
double a3 = 0.1640425613;
return a0 + a1*x + a2*x*x + a3*x*x*x;
}
|
Start with x0 = approx(t) as an initial guess. To get the Newton approximation equation, we need the derivative of f(x) = t - 2x. So df/dx = d/dx(t - 2x) = d/dx(t - eln(2) x) = - ln(2) eln(2) x = - ln(2) 2x. Starting with the guess x0, the Newton equation for the new guess x1 is: