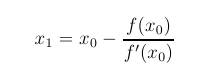
CS3343/3341 Analysis of Algorithms Spring 2012 Weird Topic |
Newton's Method, Part 2
General Square Root |
Newton's method is amazing because each iteration (each loop) doubles the number of correct digits of the answer.
Newton's Method is used to find successive approximations to the roots of a function. If the function is y = f(x) and x0 is close to a root, then we usually expect the formula below to give x1 as a better approximation. Then you plug the x1 back in as x0 and iterate.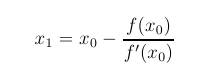
A number of web pages explain how the above formula for Newton's method is derived. For example:
Historically, Newton's method has been used in software and in hardware for two impressive tasks: carry out division, and compute the square root. Early in the computer era addition (and subtraction, of course), along with multiplication, were implemented in hardware. Division was quite a bit harder to implement. Think about the multiplication and division by hand that you (surely) learned early in school. Programming multiplication would be relatively straightforward compared with division, which involved successively guessing the next digit to use for the quotient. To quote from Knuth (Vol. 2, page 251):
Double-precision floating division is the most difficult routine, or at least the most frightening prospect we have encountered so far in this chapter. Actually, it is not terribly complicated once we see how to do it; ...Because of such difficulties, Newton's method was often used. The square root can be implemented using Newton's method with software or hardware almost identical to an implementation of division. Sometimes these were combined into one unit. High performance square root algorithms still use Newton's method. (See The Standard C Library, by P.J. Plauger, 1991, which is the best-known reference of this type.) Here are the steps in this process:

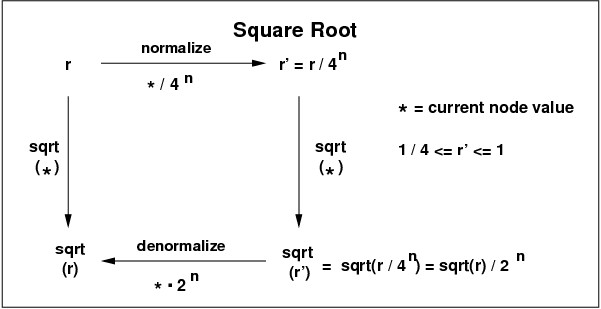
Square Root of Two. Here there is no normalization, and only a specific square root. It would not be hard to add normalization and square roots of arbitrary numbers.
This page shows the rapid convergence of Newton's method. In this case, 9 loop iterations yield 391 decimal digits of the answer.Square Root. The square root of an arbitrary double r > 0 using normalization as explained above.
Division. The reciprocal of an arbitrary positive double d > 0 using normalization.
Square Root Compared with Division. This page shows the remarkable similarity between the code for division and that for square root.