(Textbook. Click for information.)

CS 3343/3341  Analysis of Algorithms  Spring 2012  Recitation 10  Graph Search     Very Partial Answers

This Recitation didn't seem too hard, but there was a lot of programming. I might say something about the answer to Part D, which I thought was more interesting than the others.

Topological Sort Using Indegree. It seems obvious to me that the basic method works. I think it was clear to a number of you.

First you need an indegree field in the vertex class. This needs to be set properly. It can easily be done as you input the graph -- I did it in a separate pass through the graph, and either of these is O(V+E). Then many of you realized that you needed some data structure (list, stack, queue) to hold those vertices with current indegree 0. Go through the vertices once putting all that have indegree 0 into the list. Then the main loop grabs any vertex v from the list, outputs it as the next item in the topological sort, and uses v's adj. list to decrement all the vertices on directed edges going from v. Any of these vertices that newly have indegree 0 must be put on the list. If you run out of vertices on the list before sorting them all, there is a cycle. This second part is also O(V+E).

At least one reasonable student was thinking that O(V+E) meant you could only go through the vertices once and the edges once. But O(V+E) allows any fixed constant times V+E, although the same constant must work for any size graph.

I think this works. Fairly easy to program, as these things go.

• Breadth-first Search (BFS).
• Print-Path (using BFS).
• Depth-first Search (DFS).
• Topological Sort (using DFS).

I am also asking you to construct and run an alternative topological sort algorithm:

• Alternative Topological Sort. Your text's Exercise 22.4-5, page 615.

1. Breadth-first Searches and PrintPaths. This part can be done with a single run, using the 48-node graph of state capitals. For this run, the distances (in miles, edgeDist field) between capitals are not used. However, you have d, pi and color fields as part of the vertex data. These are described in your text under "Breadth-first Search". Here are four input files with the raw data. You may use any of these.
   1. capsdist.txt. The old file with vertices of edges and distance (miles) between them.
   2. capsdist.txt. Same as the a file, but with an initial record holding "48", the number of vertices.
   3. caps.txt.Same as the a file, but without the distance values, only specifying the vertices.
   4. capsh.txt. Same as the c file, but with an initial record holding "48", the number of vertices.

   Your run for this part must include:

   1. the breadth-first search,
   2. printing of the list of vertices with the vertex data (values of the d and pi fields for each vertex, showing the course of the search and defining the breadth-first spanning tree), and
   3. printing a shortest path going mostly across the country (your choice). Notice that for the shortest path, the distance is 1 for each edge.

2. Depth-first Search of the 48-capitals graph. For this search, each vertex should have pi, color, d, and f fields as specified in your text. Notice that the d is used differently here, for "time discovered", while f stands for "time finished". (A global variable time provides a simulation of time passing during the algorithm.)

   Your run for this part must include:

   1. the depth-first search,
   2. printing of the list of vertices with the vertex data (values of the d, f, and pi fields for each vertex, showing the course of the search and defining the depth-first spanning tree).

3. Depth-first Search and topological sort. In this part you must work with two examples from your text.
   1. First is the dag in Figure 22.7 on page 613. For use in our program, I've numbered the 9 vertices as: undershorts:0, socks:1, watch:2, pants:3, shoes:4, belt:5, shirt:6, tie:7, jacket:8. ["Undershorts"! What the hell? I looked this up in my paper dictionary, since it's obviously some archaic term. It said "See short 4b". OK, under that reference, it said: "pl: short drawers". What? This sounds actively scary. Whatever this guy is wearing, he can't pull it on over his shoes!]
      

      Notice that this is a directed graph, so we don't enter edges in both directions as we did before. It is also acyclic, meaning that there are no non-trivial loops. This is what your text calls a "dag", a "directed acyclic graph". The DFS has to start over again at several vertices, and the spanning tree is a spanning forest consisting of several trees. Here are two input files with the edges: clothing.txt, and clothingh.txt with an initial record holding "9".

      In order to carry out the topological sort, you add a single print after the part of the DFS that gives each f field its value. This will print the vertices in reverse order from the order of topological sort. (See your text, page 613. You don't need to bother putting them into a linked list as your text suggests.) Notice that in general there will be many different correct topological sorts, so you should not expect to get the order shown in the image above.

   2. The second dag for a DFS and topological sort is from Figure 22.8 on page 615. The figure shows vertices labeled with letters from m to z, but in the data below, these are integers from 0 to 13.
      

      Here are two input files with the edges: dag.txt, and dagh.txt with an initial record holding "14". In this case the spanning tree is again a spanning forest, with three separate trees. Here again you should give the vertices in reverse order of a topological sort.

4. Alternative Topological Sort (using the vertex in-degree)

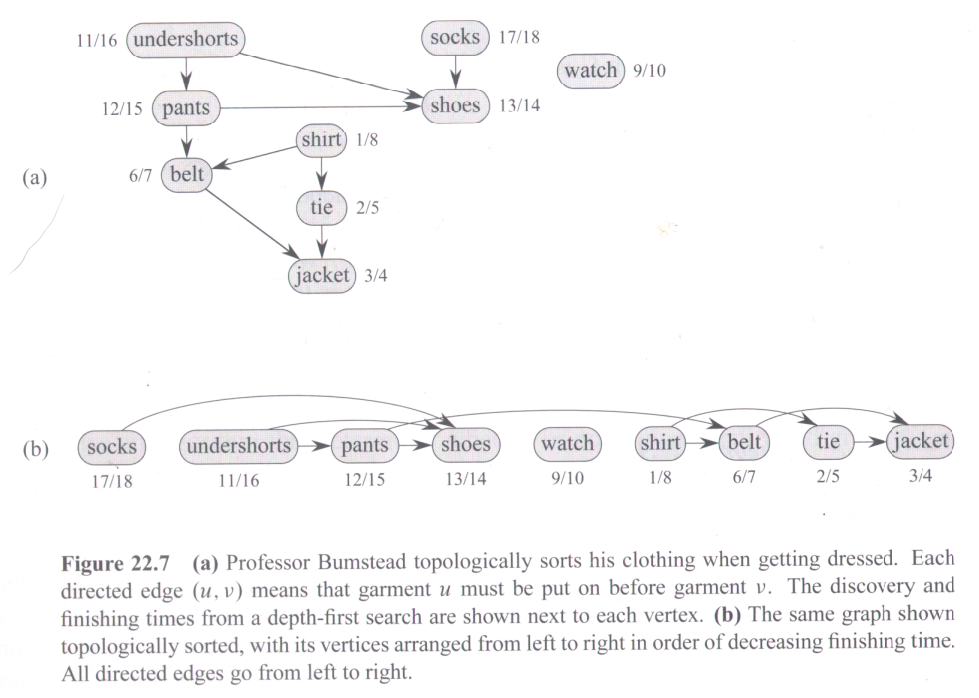
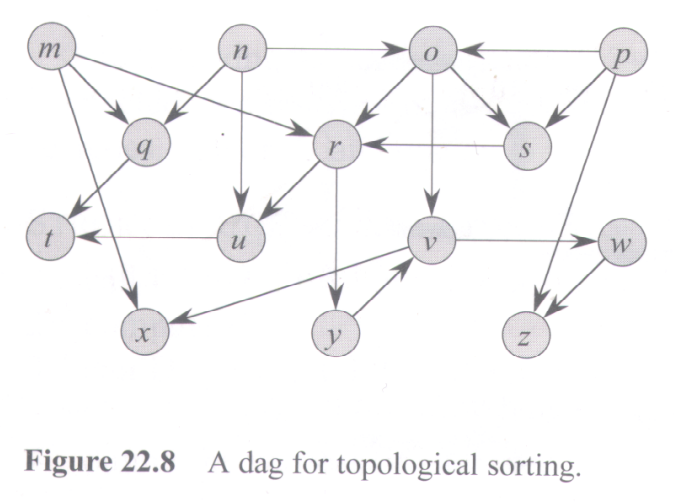
   "Exercise 22.4-5, page 615: Another way to perform topological sorting on a directed acyclic graph G = (V, E) is to repeatedly find a vertex of in-degree 0, output it, and remove it and all its outgoing edges from the graph. Explain how to implement this idea so that it runs in time O(V + E). What happens to this algorithm if G has cycles?" [Here "in-degree" of a given vertex means the number of edges coming into the vertex.]

   1. This is the main interesting problem in this recitation. You must describe your algorithm in such a way that I am convinced you have something that will work. You should also try out your algorithm by hand on the second dag above, the one with 14 vertices. or perhaps discover the algorithm by working with this example. For full credit, you must argue that your algorithm runs in O(V + E) time. Be sure to answer the question about what happens if the input graph has a cycle.

   2. Finally, implement this algorithm in Java or C. Independent of an implemenion, you must also include the description called for above. Your implementation is expected to match what it called for in your text's exercise above. You should run this with both examples above: the 9 vertex clothing example, and the 14 vertex dag example.