Introduction to the Design and Analysis of Algorithms
(Textbook. Click for information.)
 CS 3343/3341
 Analysis of Algorithms
 Spring 2012
 Recitation 9
 Graph Representation
    Week 10: Mar 27-Mar 29
 Due (on time): 2012-04-02  23:59:59
 Due (late):        2012-04-06  23:59:59

NOTE: OK, this "accelerated" due date has not been popular. I decided to let the date slide to the "normal" Monday due date. The part-credit due date is also now the "standard" day, Friday.

Recitation 9 should be submitted following directions at: submissions with deadlines
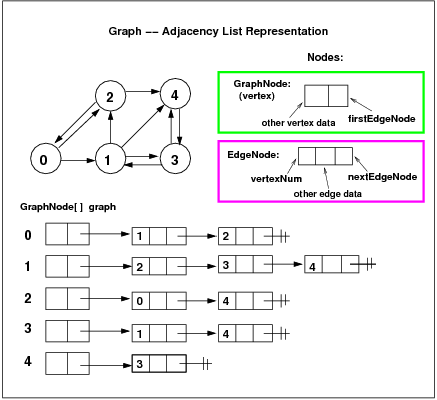
  • 2012-04-02  23:59:59 (that's Monday, 02 April 2012, 11:59:59 pm) for full credit.
  • 2012-04-06  23:59:59 (that's Friday, 06 April 2012, 11:59:59 pm) for 75% credit.

Introduction. In this recitation you will work on a program that will create an internal, linked list representation of an arbitrary graph. The graph can be either directed or undirected, with vertices and edges. There can be information attached to the edges as well as to the vertices. We want to be able to carry out algorithms on these graphs.

One of the example graphs we will work with consists of the 48 US state capitals, with distances between them. Here is diagram of this graph, with the capitals (vertices) given as integers from 0 to 47. (See here for the names of capitals. The example and layout are due to Donald Knuth.)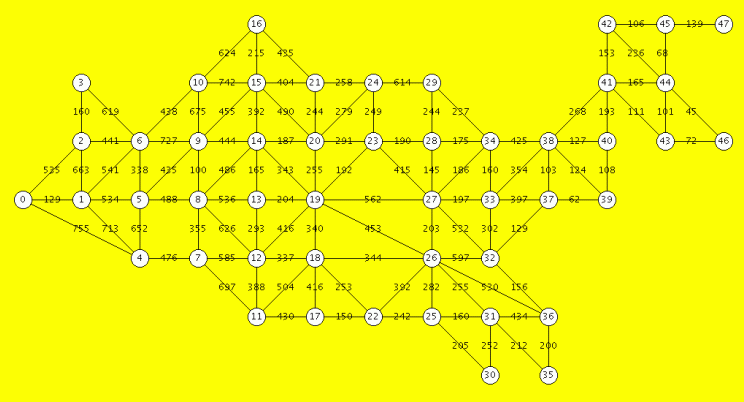


US state capitals (larger picture: here)

The Representation. For this recitation, you are to write a Java or C program that reads data about a graph (such as the one above) and constructs an adjacency list internal representation of this graph. (See your text, pages 589-592. The alternative to this representation is the adjacency matrix representation, which has advantages and disadvantages when compared with adjacency lists.) Here is a picture of this representation:


Click picture for larger image (.png) or here for full size (.pdf).

You should realize that I wanted the code to be as simple as possible. In particular, this means not using accessor functions for class data members, but instead public data members. (In fact, a version using accessor methods is what I wrote first.) Besides simplicity, this approach matches the algorithms in your text more closely. It is possible to have far more sophisticated graph software, as for example with the programs that Dr. Maynard uses that allow the graph to change dynamically, add or delete vertices and edges during run-time. Instead we will apply algorithms to a fixed graph, with a fixed set of vertices, numbered 0, 1, 2, 3, ..., and a fixed set of edges.

The example in the diagram above is a directed graph. For an undirected graph we just use a directed edge in each direction. (The graph of capitals above is undirected.) Again in the diagram above, the vertices (nodes of the graph) are represented by an array of nodes: GraphNode [ ] graph = new GraphNode[5];. The edges are represented by the vertices at either end; the first vertex is the vertex in the array and the second vertex is in the linked list of vertices linked to from the first vertex. It's very important to keep clear that, even though the linked list gives vertex numbers, these all represent edges. The vertices are all those at the end of a directed or undirected edge from the first vertex. These vertices in the linked list can appear in any order.

Recitation 9 Requirements. There are five parts:

  1. Complete the program below that will convert an arbitrary graph into an internal adjacency list form. This involves completing the function insert that inserts nodes into the adjacency lists.
  2. Write a printGraph function that will print the details of the adjacency lists.
  3. Write an edgeDistance function that will return the specific weight attached to edges for the example of the 48 US capitals.
  4. Write a pathLength function that will determine the length of a given path, using edgeDistance.
  5. Run this program for the special case of the graph of the 48 US capitals. This includes printing the graph with printGraph and determining the lengths of three Hamiltonian paths given below, using pathLength.
Your program should start by reading a file of pairs of vertices (in this case integers from 0 to 47 inclusive), each pair representing an edge, along with the distance (an integer) between them: capsdisth.txt. This file starts with a "48" for the number of vertices in the graph, to match the Java code below (which I changed a few days ago). The corresponding C program (graph.c) has the "48" hardwired into the code, so for this program you should use the file capsdist.txt which does not have the initial "48". (Alternatively, you can allocate the graph array in the C program dynamically, as with the Java version.)

Each edge is listed only once, but must be entered twice in each direction because this is an undirected graph. Your program needs to read this data and construct an internal representation similar to the diagram above. Below I am giving you code for one version of this program, including everything but the parts that construct the adjacency list (and insert the distances). In the skeleton program below, the comments in red mark places where you need to or may want to insert code.

The edgeDistance function. This assignment also asks you to write a function edgeDistance, which, given as input parameters the numbers of two vertices, will return the edge distance between them in case the vertices form an edge from the first to the second. Otherwise the function should return -1.

The pathLength function and 3 Hamiltonian paths. The program below includes the definitions of three Hamiltonian paths in the graph. You should determine the lengths of each of the three/

Below is the Java program for this assignment. A version of this program in C is graph.c.

Graph construction: 48 mainland US capitals. Data from file: capsdist.txt
// Graph.java: set up graphs data structure
//  Uses adjacency list representation
import java.io.*;
import java.util.Scanner;
public class Graph {
   private int count; // number of nodes
   private Scanner sc; // input file name
   private GraphNode[] graph; // the graph

   private void err(int code) {
      System.exit(code);
   }

   public Graph(String fileName) {
      int num1 = 0, num2 = 0, num = 0;
      try {
         sc = new Scanner(new
            File(filename));
      }
      catch (Exception exception ){err(1);}
      // get count = num of vertices
      if (sc.hasNextInt())
         count = sc.nextInt();
      else err(2);
      graph = new GraphNode[count];
      for (int i = 0; i < count; i++)
         graph[i] = new GraphNode();
      while (sc.hasNextInt()) {
         num1 = sc.nextInt();
         if (sc.hasNextInt())
            num2 = sc.nextInt();
         else err(2);
         if (sc.hasNextInt())
            num = sc.nextInt();
         else err(3);
         // undirected, insert both ways
         insert(num1, num2, num);
         insert(num2, num1, num);
     }
   }

   private void insert(int num1, int num2,
           int dist) {
      // patch the new node in at the start
      if (graph[num1].firstEdgeNode==null){
         // create new adjacency list, with
         // a node for num2, its only entry
      }
      else {
         // patch in a node for num2 at the
         // start of the existing adj list
      }
   }

   public void printGraph() {
      // print the data in the graph,
      // perhaps in the form below
   }

   public int edgeDistance(int v1, int v2) {
      // if (v1, v2) is an edge
      // return edgeDist of this edge
      // otherwise return -1
   }

   public int pathLength(int[] path) {
      // calculate and return the length
      // of the path specified by the input
      // parameter.  If the "path" includes
      // a non-edge return -1
   }

}

// GraphNode.java: node for graph's vertex
//  Holds vertex info, link to adj. list
public class GraphNode {
   public EdgeNode firstEdgeNode;//adj.list
   // other vertex info here

   // probably want to use a constructor
}

// EdgeNode.java: holds graph's edge info
//  Implement adjacency list
public class EdgeNode {
   public int vertexNum; //head end of edge
   public EdgeNode nextEdgeNode;//next node
   public int edgeDist; // edge length
   // other edge info here

   // probably want to use a constructor
}

// GraphMain.java: Controls Graph Program
import java.io.*;
public class GraphMain {
   public static void main(String[] args) {
       Graph graph = new Graph(
             "capsdisth.txt");
       graph.printGraph();

      // three Hamiltonian paths
      int[] Ham1 =
       {47,45,42,44,46,43,41,40,39,37,33,38,
        34,28,29,24,21,16,10,15,20,23,27,32,
        26,36,35,31,30,25,22,18,17,11, 7,12,
         8,13,19,14, 9, 5, 4, 0, 2, 1, 6, 3};
      int[] Ham2 =
       {47,45,42,44,46,43,41,40,38,39,37,32,
        36,35,31,30,25,22,17,11,12,18,26,27,
        33,34,29,28,23,19,13,14,20,24,21,15,
        16,10, 6, 5, 9, 8, 7, 4, 1, 0, 2, 3};
      int[] Ham3 =
       {47,45,42,44,46,43,41,40,39,37,33,32,
        36,35,31,30,25,26,27,28,23,20,19,18,
        22,17,11,12,13,14,15, 9, 8, 7, 4, 5,
         1, 0, 2, 3, 6,10,16,21,24,29,34,38};
      System.out.println("Path length: " + 
         graph.pathLength(Ham2));
   }
}
Pairs of Cities & Distances (Edges and weights)
file: capsdist.txt
48
0  4 755
0  1 129
0  2 535
1  4 713
1  5 534
1  6 541
1  2 663
2  6 441
2  3 160
3  6 619
4  7 476
4  5 652
5  8 488
5  9 435
5  6 338
6  9 727
6 10 438
7 11 697
7 12 585
7  8 355
8 12 626
8 13 536
8 14 486
8  9 100
9 14 444
9 15 455

 9 10 675
10 15 742
10 16 624
11 17 430
11 18 504
11 12 388
12 18 337
12 19 416
12 13 293
13 19 204
13 14 165
14 19 343
14 20 187
14 15 392
15 20 490
15 21 404
15 16 215
16 21 435
17 22 150
17 18 416
18 22 253
18 26 344
18 19 340
19 26 453
19 27 562
19 23 192
19 20 255

20 23 291
20 24 279
20 21 244
21 24 258
22 25 242
22 26 392
23 27 415
23 28 190
23 24 249
24 29 614
25 30 205
25 31 160
25 26 282
26 31 255
26 36 530
26 32 597
26 27 203
27 32 532
27 33 197
27 34 186
27 28 145
28 34 175
28 29 244
29 34 237
30 31 252
31 35 212

31 36 434
32 36 156
32 37 129
32 33 302
33 37 397
33 38 354
33 34 160
34 38 425
35 36 200
37 39 62
37 38 103
38 39 124
38 40 127
38 41 268
39 40 108
40 41 193
41 43 111
41 44 165
41 42 153
42 44 236
42 45 106
43 46 72
43 44 101
44 46 45
44 45 68
45 47 139

Here is one possible version of the data that your printGraph() function should produce:

Complete Structure of the Internal Graph Representation
(undirected graph, so each edge appears twice)
First
vertex		Second vertices of edges and distances,
starting with the first vertex at the left
0:  [2,535],[1,129],[4,755]
1:  [2,663],[6,541],[5,534],[4,713],[0,129]
2:  [3,160],[6,441],[1,663],[0,535]
3:  [6,619],[2,160]
4:  [5,652],[7,476],[1,713],[0,755]
5:  [6,338],[9,435],[8,488],[4,652],[1,534]
6:  [10,438],[9,727],[5,338],[3,619],[2,441],[1,541]
7:  [8,355],[12,585],[11,697],[4,476]
8:  [9,100],[14,486],[13,536],[12,626],[7,355],[5,488]
9:  [10,675],[15,455],[14,444],[8,100],[6,727],[5,435]
10: [16,624],[15,742],[9,675],[6,438]
11: [12,388],[18,504],[17,430],[7,697]
12: [13,293],[19,416],[18,337],[11,388],[8,626],[7,585]
13: [14,165],[19,204],[12,293],[8,536]
14: [15,392],[20,187],[19,343],[13,165],[9,444],[8,486]
15: [16,215],[21,404],[20,490],[14,392],[10,742],[9,455]
16: [21,435],[15,215],[10,624]
17: [18,416],[22,150],[11,430]
18: [19,340],[26,344],[22,253],[17,416],[12,337],[11,504]
19: [20,255],[23,192],[27,562],[26,453],[18,340],[14,343],[13,204],[12,416]
20: [21,244],[24,279],[23,291],[19,255],[15,490],[14,187]
21: [24,258],[20,244],[16,435],[15,404]
22: [26,392],[25,242],[18,253],[17,150]
23: [24,249],[28,190],[27,415],[20,291],[19,192]
24: [29,614],[23,249],[21,258],[20,279]
25: [26,282],[31,160],[30,205],[22,242]
26: [27,203],[32,597],[36,530],[31,255],[25,282],[22,392],[19,453],[18,344]
27: [28,145],[34,186],[33,197],[32,532],[26,203],[23,415],[19,562]
28: [29,244],[34,175],[27,145],[23,190]
29: [34,237],[28,244],[24,614]
30: [31,252],[25,205]
31: [36,434],[35,212],[30,252],[26,255],[25,160]
32: [33,302],[37,129],[36,156],[27,532],[26,597]
33: [34,160],[38,354],[37,397],[32,302],[27,197]
34: [38,425],[33,160],[29,237],[28,175],[27,186]
35: [36,200],[31,212]
36: [35,200],[32,156],[31,434],[26,530]
37: [38,103],[39,62],[33,397],[32,129]
38: [41,268],[40,127],[39,124],[37,103],[34,425],[33,354]
39: [40,108],[38,124],[37,62]
40: [41,193],[39,108],[38,127]
41: [42,153],[44,165],[43,111],[40,193],[38,268]
42: [45,106],[44,236],[41,153]
43: [44,101],[46,72],[41,111]
44: [45,68],[46,45],[43,101],[42,236],[41,165]
45: [47,139],[44,68],[42,106]
46: [44,45],[43,72]
47: [45,139]

Revision date: 2012-03-21. (Please use ISO 8601, the International Standard.)