Textbook

CS 3343  Analysis of Algorithms  Fall 2012  Recitation 11  A Few Answers  In-Class Problems     Week 11: Nov 06-Nov 08

You must follow the Rules for In-Class Recitations.

1. You are to start with one of the two programs above, either the Java on or the C one. (The programs are as identical as I could make them, but the Java one is probably easier to understand and to modify.)
   1. Write a printGraph function that will print the details of the adjacency lists, as shown on the page above (but doesn't have to be neat or pretty).
   2. Write an edgeLength function that will return the specific weight attached to edges for the example of the 48 US capitals.
   3. Write a pathLength function that will determine the length of a given path, using edgeLength.
   4. Run this program for the special case of the graph of the 48 US capitals. This includes printing the graph with printGraph and determining the lengths of three Hamiltonian paths given below, using pathLength.

   The three functions above are described more thoroughly in the following outlines, and declarations for the paths are also given below:

   In Java Language	In C Language
   public void printGraph() { // print the data in the graph, // perhaps in the form below } public int edgeLength(int v1, int v2) { // if (v1, v2) is an edge // return edgeLen of this edge // otherwise return -1 } public int pathLength(int[] path) { // calculate and return the length // of the path specified by the input // parameter. If the "path" includes // a non-edge return -1 }	void printgraph(struct node* graph[], int count) { // print the data in the graph, // perhaps in the form below } int edgelength(struct graphnode* graph[], int v1, int v2) { // if (v1, v2) is an edge // return edgelen of this edge // otherwise return -1 } int pathlength(struct node* graph[], int path[], int plen) { // calculate and return the length // of the path specified by the input // parameter. If the "path" includes // a non-edge return -1 }
   // three Hamiltonian paths int[] Ham1 = {47,45,42,44,46,43,41,40,39,37,33,38, 34,28,29,24,21,16,10,15,20,23,27,32, 26,36,35,31,30,25,22,18,17,11, 7,12, 8,13,19,14, 9, 5, 4, 0, 2, 1, 6, 3}; int[] Ham2 = {47,45,42,44,46,43,41,40,38,39,37,32, 36,35,31,30,25,22,17,11,12,18,26,27, 33,34,29,28,23,19,13,14,20,24,21,15, 16,10, 6, 5, 9, 8, 7, 4, 1, 0, 2, 3}; int[] Ham3 = {47,45,42,44,46,43,41,40,39,37,33,32, 36,35,31,30,25,26,27,28,23,20,19,18, 22,17,11,12,13,14,15, 9, 8, 7, 4, 5, 1, 0, 2, 3, 6,10,16,21,24,29,34,38}; System.out.println("Path length: " + graph.pathLength(Ham2));	// three Hamiltonian paths int ham1[] = {47,45,42,44,46,43,41,40,39,37,33,38, 34,28,29,24,21,16,10,15,20,23,27,32, 26,36,35,31,30,25,22,18,17,11, 7,12, 8,13,19,14, 9, 5, 4, 0, 2, 1, 6, 3}; int ham2[] = {47,45,42,44,46,43,41,40,38,39,37,32, 36,35,31,30,25,22,17,11,12,18,26,27, 33,34,29,28,23,19,13,14,20,24,21,15, 16,10, 6, 5, 9, 8, 7, 4, 1, 0, 2, 3}; int ham3[] = {47,45,42,44,46,43,41,40,39,37,33,32, 36,35,31,30,25,26,27,28,23,20,19,18, 22,17,11,12,13,14,15, 9, 8, 7, 4, 5, 1, 0, 2, 3, 6,10,16,21,24,29,34,38}; printf("Path length: %i\n", pathlength(graph, ham3, 48));

   [Here are results of the three paths:

   • Ham1: Path length: 18040 (longest)
   • Ham2: Path length: 11698 (shortest)
   • Ham3: Path length: 13619 (random)

   The link Hamiltonian Paths also gives the lengths of the above three paths.]

   ---

2. Write a recursive backtracking program that will generate all Hamiltonian paths (called HP here) on a graph. Initially I want you to use a graph defined in the file small.txt:

   Your program will be searching for all HPs starting with vertex 10. There are 66 of them. Here is an example of one of these HPs: {10,9,8,6,3,7,4,0,1,2,5}. The longest HP has length 670. Later you can try working with the graph of state capitals, but there is no requirement that you do so. (I recommend that you try just for the fun of running something larger. With luck all you would need to change is the source for the graph (and one constant in the C program). You would need to use the "head start" described below.)

   Here is an outline of what you might do:

   Each vertex (node) has to have a color, either White or Black. White means the given vertex is not yet on the current path, while Black means it is on the current path. Initially all vertices are White.

   Let the pathsearching function be hamPaths, with parameters (int u, int pathLen, int edges). Here u is the starting vertex for this call (which is a vertex in a growing HP), pathLen is the total path length so far, and edges is the number of edges so far.

   (Start of definition of function:) hamPaths(int u, int pathLen, int edges): (On entering the color of u must be White.) Set u's color to Black. (u is on the current path) For each vertex v in u's adjacency list do the following: If the color of v is White then (You need to know the edge length from u to v.) (Call hamPaths recursively using) hamPaths(v, new path length, new # of edges); (reflecting the addition of this edge to the path) (In case the color of v is Black do nothing, since the vertex is already on the current path) (Finish up the call to hamPaths:) Set color of u to White (no longer on current path) (Return from hampaths.) (Initial call:) hamPaths(10, 0, 0); (starting at ME)

   At the beginning of the call to hamPaths, if the input parameter edges has value 10 (or 48 for the 48 Capitals graph), then you are at the end of an HP. (At this point all vertices are Black, and there is nowhere for a path to go.) You might count the number of paths, and you might think about printing the path length. This wouldn't work well though because there are too many HPs. I kept track of the current longest and shortest HPs encountered up to that point, and I only printed out the data about a path in case the path was exceptional (new record for longest or shortest so far).

   Since we want to know what an HP actually was, one method is to add an integer stack, call it st. At the start of hamPaths, push u's value onto st. At the end of hamPaths, pop st. In case of an exceptional number for the length of the HP, you can print the path by printing the values on st (without popping).

   There are 2 ways to go from 10 to 8, but only one of these ways leads to any HPs. The length of this initial path is 133 and it includes 2 edges. Thus we can artificially start out from vertex 8, with the start of the path hard-wired in, using the function below.

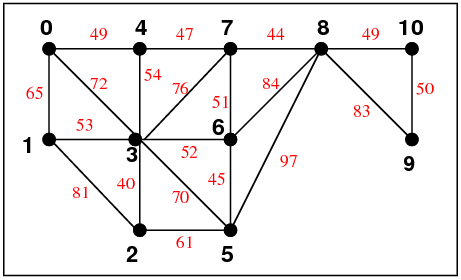
   public void hamPathsStart() { // for "small.txt" // set color of vertices 10,9 to Black // push vertices 10,9 hamPaths(8, 133, 2); }

   In the case of the 48 Capitals graph, a similar "head start" would be essential, cutting the execution time by a factor of 7. Without this change your program would likely run for days or weeks before producing any output. Here is the new start-up function:

   public void hamPathsStart() { // for 48-capitals // set color of vertices 47,46,45,44,43,42 to Black // push vertices 47,45,42,44,46,43 in that order hamPaths(41, 709, 6);); }

   Your answer to this question should be the code for the function hamPaths, along with a run showing all 66 HPs. You should also use a stack as described above to print the actual 66 HPs (or else just the actual path for the longest and the sortest HP).
   A dump of the graph and all 66 HPs are given at data.txt.
   In particular, the shortest HP and the longest are:
   16: 537: 10 9 8 7 4 0 1 3 2 5 6 (shortest)
   32: 670: 10 9 8 6 7 3 5 2 1 0 4 (longest)