CS 3343/3341
 Analysis of Algorithms 
Weird Topic
  Capitals in USA  
  Hamiltonian Paths  

[Note (added later): It is feasible to carry out a simple backtracking search of all Ham paths starting at ME. The results agree completely with Knuth's much more sophisticated methods: Hamiltonian paths.

Another interesting feature of this example came up after the page was finished. Knuth uses a second example, similar to the "all capitals", in which he adds the District of Columbia, denoted "DC" as an extra node between Maryland (MD) and Virginia (VA), with suitable edge lengths for the two new edges. I naively thought that an extra city and two extra edges should increase the number of Ham paths, but in fact this leads instead to far fewer Ham paths. With DC present, any Ham path must go through the two edges connecting MD to DC to VA, and must always skip the edge going directly from MD to VA. That gives no new Ham paths, but eliminates all the previous Ham paths (a large number of them) that didn't use the edge from VA to MD at all. In fact, the longest Ham path below doesn't use this edge while the shortest Ham path does use it. Knuth leaves this issue as a simple exercise.]

Introduction. Donald Knuth in his book Combinatorial Algorithms works with an example graph consisting of the 48 state capitals (excluding Hawaii and Alaska), with the normal driving distances between them. A path in a graph is a sequence of vertexes, each connected to the next with an edge. A simple path includes each vertex at most once. A Hamiltonian path includes each vertex exactly once. (Of course neither of these last two kinds of paths can cross themselves.) Finding a Hamiltonian path in a graph is an NP-complete problem. (The meaning of this will be discussed elsewhere, but in simple terms, such problems are considered intractable.) Knuth used extremely sophisticated and powerful tools (mostly tools developed by others) to arrive at his results.

Data About Paths. Any Hamiltonian path in this example must clearly start or end at ME. Knuth first considered paths from ME to CA. His tools told him that there are 437,525,772,584 distinct simple paths from ME to CA. The longest such paths are Hamiltonian, and he could show that there are 2,707,075 of them.

Then he considered Hamiltonian paths from ME to any other vertex. (A few final vertexes would be impossible.) He could show that there are 68,656,026 Hamiltonian paths from ME to any other vertex. Of these, it turns out that there is a unique longest one (of length 18040 miles) and a unique shortest one (of length 11698 miles), each ending at WA. In addition to finding the longest and shortest Hamiltonian paths, Knuth was able to calculate the average path length over all 68,656,026 paths, which is 14886.01 miles, with standard deviation 666.2. Ordinary brute-force techniques would be completely inadequate to solve these problems.

Pictures of the longest path and shortest path are given below. I also included another ("random") Hamiltonian path as a third example.


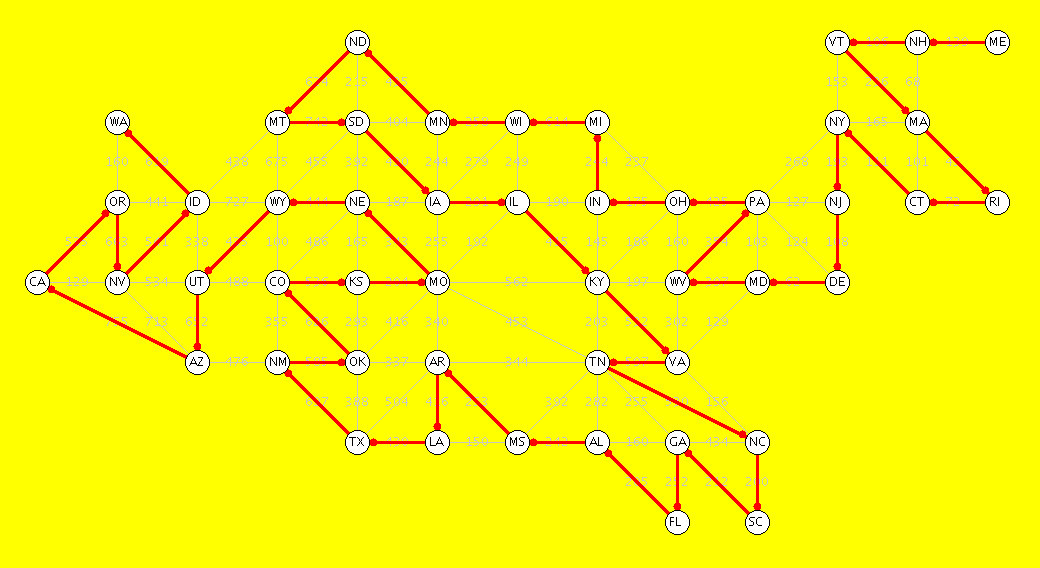
Longest Hamiltonian path, with length 18040 miles
(Click picture or here for a full size image)


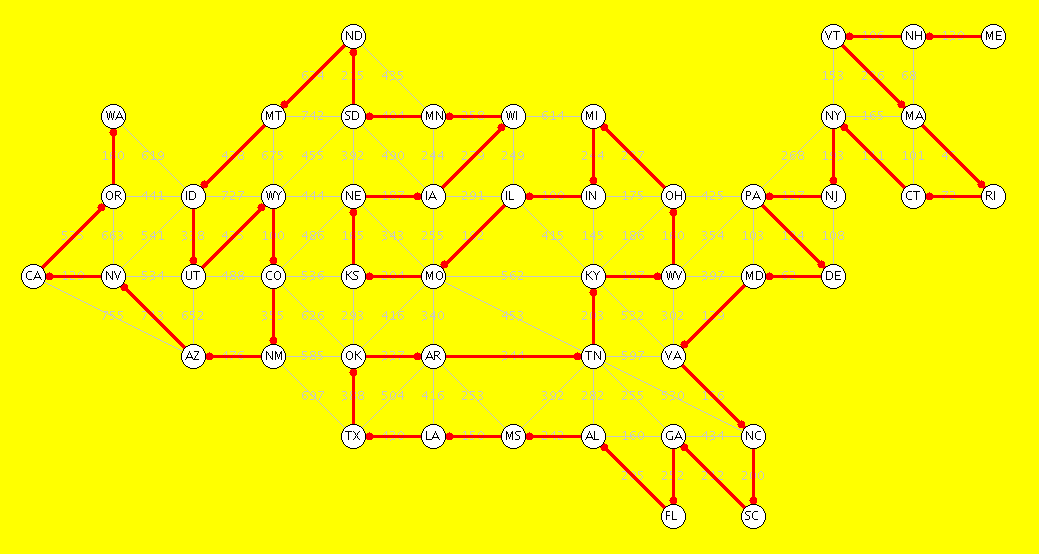
Shortest Hamiltonian path, with length 11698 miles
(Click picture or here for a full size image)


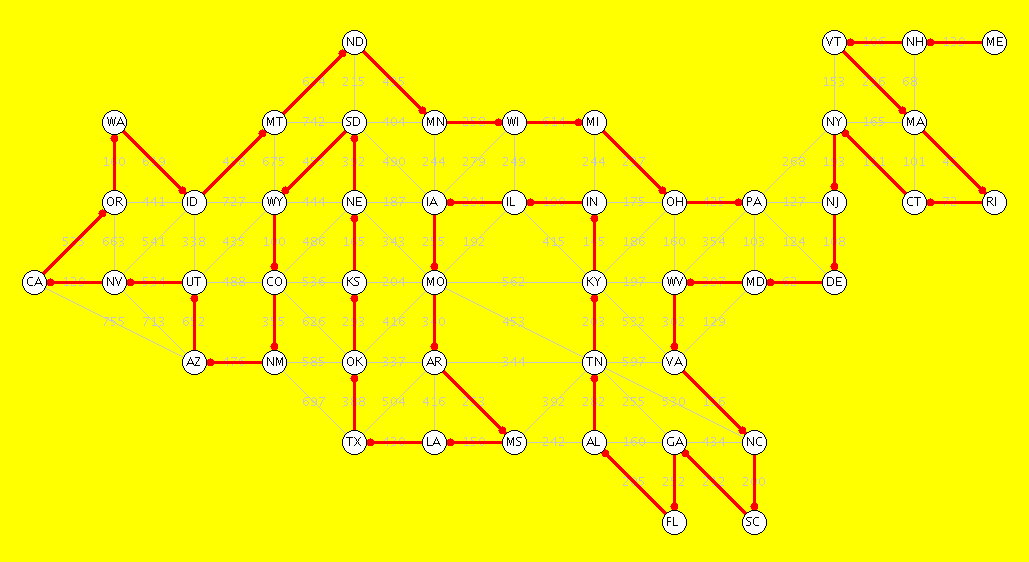
Random Hamiltonian path, with length 13619 miles
(Click picture or here for a full size image)

( Revision date: 2015-01-09. Please use ISO 8601, the International Standard Date and Time Notation.)