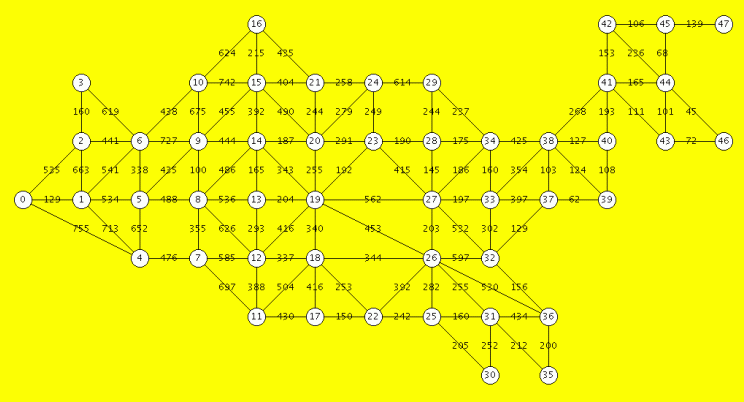
US state capitals (larger picture: here)
CS3343/3341 Analysis of Algorithms |
Graph Representation |

| Graph construction: 48 mainland US capitals. Data from file: capsdist.txt | |||||||||
|---|---|---|---|---|---|---|---|---|---|
// Graph.java: set up graphs data structure
// Uses adjacency list representation
import java.io.*;
public class Graph {
public int nodes; // number of nodes
public Node[] graph;
public Graph(int n) {
nodes = n;
graph = new Node[nodes];
for (int i = 0; i < nodes; i++)
graph[i] = new Node();
}
// insertEdge: insert directed edge
public void insertEdge(int num1, int num2,
int len) {
// patch the new node in at the start
graph[num1].firstEdge = new Edge(num2,
graph[num1].firstEdge, len);
}
| // GraphMain.java: Controls Graph Program
import java.io.*;
import java.util.Scanner;
public class GraphMain {
private static void err(int code) {
System.exit(code);
}
public static void main(String[] args) {
int nodes = 0;
Scanner sc = null; // compiler wants
int num1 = 0, num2 = 0, len = 0;
try {
sc = new Scanner(new
File("capsdist.txt")); // file
}
catch (Exception exception ) { err(1); }
if (sc.hasNextInt())
nodes = sc.nextInt();
else err(2);
Graph graph = new Graph(nodes);
// get vertices = num of vertices
while (sc.hasNextInt()) {
num1 = sc.nextInt();
if (sc.hasNextInt())
num2 = sc.nextInt();
else err(2);
if (sc.hasNextInt())
len = sc.nextInt();
else err(3);
// undirected, insert both ways
graph.insertEdge(num1, num2, len);
graph.insertEdge(num2, num1, len);
}
}
}
| ||||||||
| Complete Structure of the Internal Graph Representation (undirected graph, so each edge appears twice) | |
|---|---|
| First vertex | Second vertices of edges and distances, starting with the first vertex at the left |
0: [ 2,535],[ 1,129],[ 4,755] 1: [ 2,663],[ 6,541],[ 5,534],[ 4,713],[ 0,129] 2: [ 3,160],[ 6,441],[ 1,663],[ 0,535] 3: [ 6,619],[ 2,160] 4: [ 5,652],[ 7,476],[ 1,713],[ 0,755] 5: [ 6,338],[ 9,435],[ 8,488],[ 4,652],[ 1,534] 6: [10,438],[ 9,727],[ 5,338],[ 3,619],[ 2,441],[ 1,541] 7: [ 8,355],[12,585],[11,697],[ 4,476] 8: [ 9,100],[14,486],[13,536],[12,626],[ 7,355],[ 5,488] 9: [10,675],[15,455],[14,444],[ 8,100],[ 6,727],[ 5,435] 10: [16,624],[15,742],[ 9,675],[ 6,438] 11: [12,388],[18,504],[17,430],[ 7,697] 12: [13,293],[19,416],[18,337],[11,388],[ 8,626],[ 7,585] 13: [14,165],[19,204],[12,293],[ 8,536] 14: [15,392],[20,187],[19,343],[13,165],[ 9,444],[ 8,486] 15: [16,215],[21,404],[20,490],[14,392],[10,742],[ 9,455] 16: [21,435],[15,215],[10,624] 17: [18,416],[22,150],[11,430] 18: [19,340],[26,344],[22,253],[17,416],[12,337],[11,504] 19: [20,255],[23,192],[27,562],[26,453],[18,340],[14,343],[13,204],[12,416] 20: [21,244],[24,279],[23,291],[19,255],[15,490],[14,187] 21: [24,258],[20,244],[16,435],[15,404] 22: [26,392],[25,242],[18,253],[17,150] 23: [24,249],[28,190],[27,415],[20,291],[19,192] 24: [29,614],[23,249],[21,258],[20,279] 25: [26,282],[31,160],[30,205],[22,242] 26: [27,203],[32,597],[36,530],[31,255],[25,282],[22,392],[19,453],[18,344] 27: [28,145],[34,186],[33,197],[32,532],[26,203],[23,415],[19,562] 28: [29,244],[34,175],[27,145],[23,190] 29: [34,237],[28,244],[24,614] 30: [31,252],[25,205] 31: [36,434],[35,212],[30,252],[26,255],[25,160] 32: [33,302],[37,129],[36,156],[27,532],[26,597] 33: [34,160],[38,354],[37,397],[32,302],[27,197] 34: [38,425],[33,160],[29,237],[28,175],[27,186] 35: [36,200],[31,212] 36: [35,200],[32,156],[31,434],[26,530] 37: [38,103],[39, 62],[33,397],[32,129] 38: [41,268],[40,127],[39,124],[37,103],[34,425],[33,354] 39: [40,108],[38,124],[37, 62] 40: [41,193],[39,108],[38,127] 41: [42,153],[44,165],[43,111],[40,193],[38,268] 42: [45,106],[44,236],[41,153] 43: [44,101],[46, 72],[41,111] 44: [45, 68],[46, 45],[43,101],[42,236],[41,165] 45: [47,139],[44, 68],[42,106] 46: [44, 45],[43, 72] 47: [45,139] | |