Introduction to the Design and Analysis of Algorithms
Textbook.
 CS 3343/3341
 Analysis of Algorithms
 Numerical Calculations
 Normalize & 
  Denormalize  

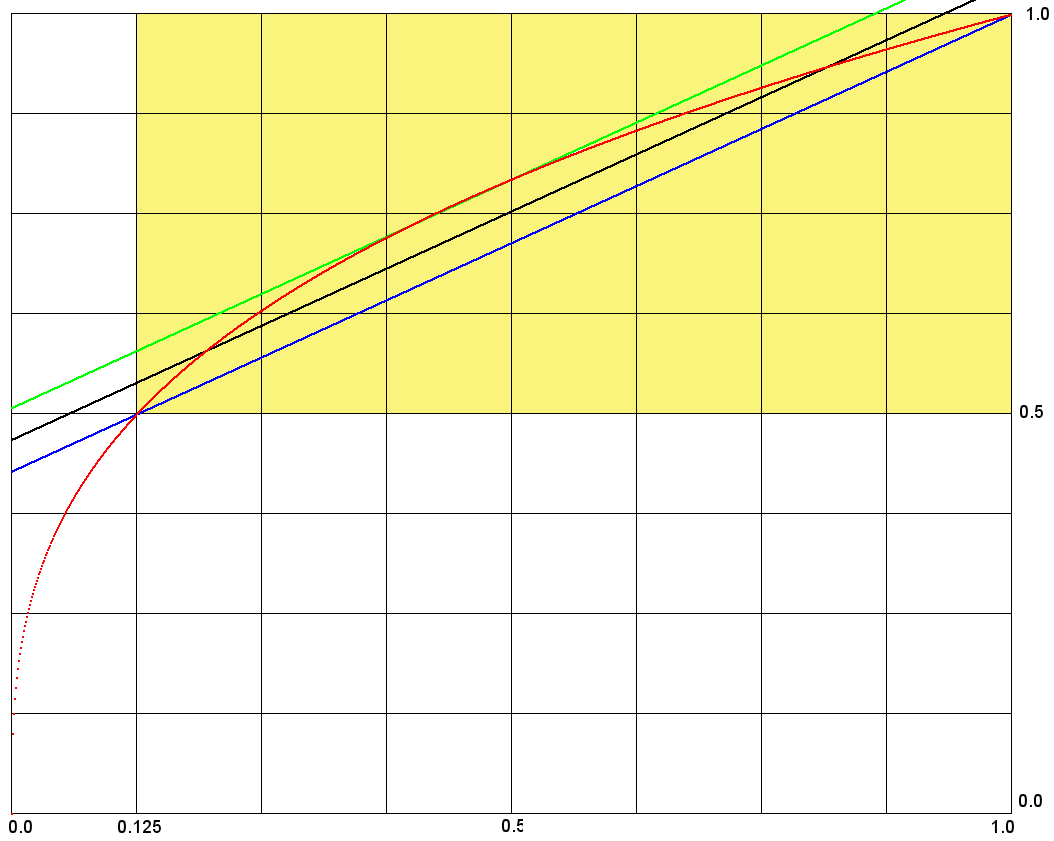
Normalize / Denormalize: This refers to a common process during numerical computations, where one shrinks the allowed input to a standard interval, and extends a solution for such an interval to a solution for all inputs. In each of the cases here one ends up with a square diagram of four functions, where the two ways of following arrows through the diagram yield the same result. Such diagrams are called commutative.

[Normalization is most frequently encountered by beginning CS students when they study the IEEE floating representation of real numbers. These are represented by base 2 scientific notation in the form:
(+|−)1.xxxxxx...2×2yyyy..., where the x's and y's are binary bits.
One bit for the sign, 11 bits for the exponent (the y's) and 52 bits for the significant bits (the x's). To convert a positive number x, say 1/3 to IEEE form, first multiply by a power of 2 so that the number x' satisfies 1 < x' < 2. So x = 1/3 = 4/3 × 2-2. Then 4/3 in binary is 1.01010101...2. The 01010101... are the x's above, and the -2 is encoded as the y's. See doubles.
This example is similar to the Division example below.]

Here are three examples on separate pages:

This page presents 2 further examples of normalization / denormalization:

  • Cube root,
  • f(x) = 2x

Cube root: Here is another example, presented as the four problems 1 through 4 below, with some comments in red after problems:

  1. Mimic what we did for square root to find the cube root. We start with r > 0. We want r1/3. We will normalize into the interval [1/8,1] by dividing by 8n for suitable n. Do up the square diagram, with r, r0=r/8n, r01/3, and r1/3 in the four corners (clockwise). Finish up all the other details about the diagram, following the pattern for square root.


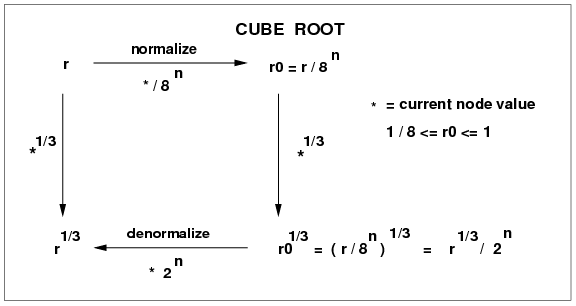
    Click box or here for full size image.

    [Some of you wrote 8n/3 for the denormalizing factor, without simplifying it to 2n. But this misses a big reason for the whole approach: that it's efficient to multiply or divide by a power of 2 on our hardware. The reason for choosing 8n for normalizing was to achieve this simple denormalizing factor.]

  1. Continuing the problem above, show how to use Newton's Method to find r1/3. Use the function f(x) = r - x3. You need to know that f ' (x) = - 3 * x2. Don't write any code, but just produce the Newton's iteration formula. If r=27 and x0=2.9, calculate by hand the next approximation x1.

    [ x1 = x0 - f(x0) / f ' (x0)
        = x0 - (r - x03) / (-3*x02)
        = x0 + (r - x03) / (3*x02)
        = x0 + r / (3*x02) - x03 / (3*x02)
        = (2/3)*x0 + r / (3*x02) =
        = (2/3)*2.9 + 27 / (3*(2.9)2) =
        = 1.9333333333 + 27 / 25.23 = 3.0034879

    The above calculation shows that if we start with x0 = 2.9, within 0.1 of the cube root of 27 which is 3, then the next approximation x1 = 3.0034879, within about 0.0035 of the cube root.

    Here is a short program: 

    #include <stdio.h>
int main() {
   double x0=2.9, x1, r=27;
   int i;
   for (i = 0; i < 10; i++) {
     x1 = (2./3.)*x0 + r / (3.*x0*x0);
     printf("i:%2i, r: %.4f, x1: %.16f\n", i, r, x1);
     x0 = x1;
   }
}
i: 0, r: 27.0000, x1: 3.0034879112168054
i: 1, r: 27.0000, x1: 3.0000040488977464
i: 2, r: 27.0000, x1: 3.0000000000054645
i: 3, r: 27.0000, x1: 3.0000000000000000

    3. Calculate the approximation function:

    Here we want to approximate the function:

    y = x^(1/3),
        for 1/8 < x < 1

    The red curve is this function. The blue line is the chord between the two endpoints, and the green line is another parallel line tangent to the curve. The black line is what we want, halfway between the other lines. This last line has the equation:

    y=0.571428*x+0.4682788,
        for 1/8 < x < 1

    For each x value, we set x0 equal to the value above as the initial guess for Newton's method.

    		  

    4. Program implementing the cube root as above: Cube Root Program. (This program was very quickly adapted from the similar square root program at: SquareRoot/Division Program.

Calculate the function f(x) = 2x: Here is a final example, the inverse of log base 2:

For this question we want to calculate a function as we did with square root, reciprocal, and log base 2. This time the function is f(x) = 2x, that is, 2 to the power x. This problem is only concerned with the normalization and denormalization. Separately, we would use a series to calculate 2x for 0 <= x <= 1, but that isn't part of this problem.

You are to draw the square diagram similar to the ones we had in the other 3 examples. Remember that we are implementing the function 2x. Start with x in the upper left corner. Then the "normalized" value x0 is found by taking floor(x) and subtracting it from x. (Here floor(x) is the largest integer value less than or equal to x.) For example, if x = 7.3, then x0 = 0.3, and if x = -5.6, then x0 = 0.4.

  1. Explain the the second example above: if x = -5.6, why is x0 = 0.4?
    [ floor(-5.6) = -6, so x - floor(x) = -5.6 - (-6) = -5.6 + 6 = 0.4 ]

  2. Carefully fill in the rest of the diagram, using variables, rather than specific numbers. (One key step is determining the denormalization formula.)

         x = input double, m = floor(x)      * = node value

             * - m
   x  --------------------> x0 = x - m
   |                         |
   |                         |
   |                         |
   |                         |
 * |                         |  *
2  |                         | 2
   |                         |
   |                         |
   |                         |
   V                         V
    x                         x0    (x - m)    x  /  m
   2  <--------------------- 2   = 2        = 2  /  2
                      m
           * (times) 2

  3. Trace through the diagram using the initial value x=6.5, and carrying specific numbers all the way through the diagram. (Remember that a positive number to the 0.5 power is just the square root of the number.)

       6.5 = input double, 6 = floor(6.5)        * = node value

             * - 6
  6.5 --------------------> 0.5 = 6.5 - 6
   |                         |
   |                         |
   |                         |
   |                         |
 * |                         |  *
2  |                         | 2
   |                         |
   |                         |
   |                         |
   V                         V
   6.5                        0.5    (6.5 - 6)    6.5  /  6
  2  <---------------------- 2    = 2        =   2    /  2
                      6
           * (times) 2

Here 26.5 is computed by
normalizing 6.5 to 0.5, calculating 20.5,
and denormalizing by multiplying by 26 = 64.
Thus 26.5 = 20.5 (times) 26.
We would use a series to calculate 20.5, and
just as before, we only need to calculate 2x

for 0 <= x <= 1.  For very large x or for negative
x with large absolute value, the series wouldn't work, so
this normalization is necessary. Finally, we would get
20.5 = 1.41421356 (using the series), and 

26.5 = 1.41421356 * 64 = 90.50966799
(using the normalization/denormalization).

(In at least some places, this is the way 2x
is actually calculated.)

( Revision date: 2015-01-08. Please use ISO 8601, the International Standard.)