See Newton's Method for a general discussion.

See Newton's Method, Part 1, Sqrt(2) for a discussion of the use of Newton's Method to calculate the square root of two.

Historically, Newton's method has been used in software and in hardware to compute the square root. High performance square root algorithms still use Newton's method. (See The Standard C Library, by P.J. Plauger, 1991, which is the best-known reference of this type.)

Here is a diagram showing the steps in this process. The diagram is followed by a description of each step.

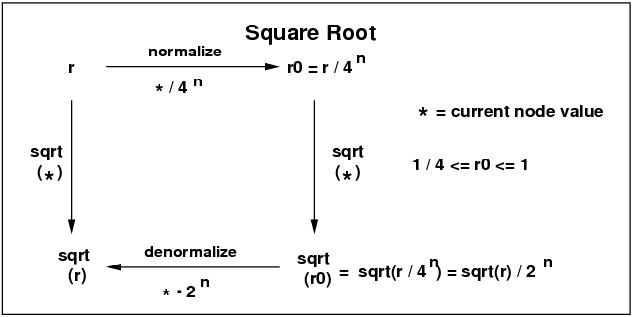
1. Normalization: Start with a number r, where we want sqrt(r). First normalize the input to some small range using powers of 2. With binary floating point numbers, multiplication or division by a power of two only needs to adjust the exponent part of the number, which can be done very quickly.

   For square root, transform r into a normalized value r0 that lies in the interval from 0.25 to 1, that is, 0.25 ≤ r0 ≤ 1. For the transformation multiply by an even power of two. The power can be either positive or negative, that is n can be either positive or negative. (At the end, denormalize by dividing by the square root of the normalizing factor.)

   In this way we reduce the problem of finding an arbitrary square root to the simpler problem of finding the square root of a number between 0.25 and 1.

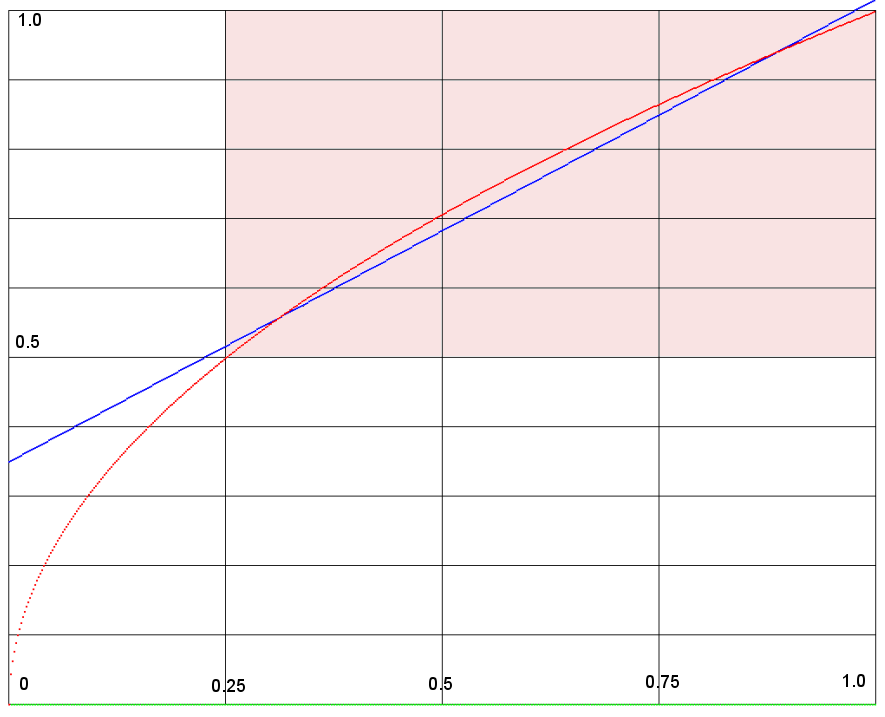
2. Initial Approximation: Use a simple approximating function on the normalized interval. In this case, using notation from the picture above, approx(r0) = 0.66666*r0 + 0.3506, for 0.25 ≤ r0 ≤ 1. Here is a graph of the approximation. The red line shows the function sqrt(x), while the blue line gives the approximation. (A line joining (0.25, sqrt(0.25)) and (1, sqrt(1)) has slope 2 / 3. The approximation is a line with that slope that minimizes the average distance from the line to the function. The area at issue is in pink below.)
   

3. Basic Calculation of Square Root of the Normalized Number: Use Newton's method to converge to the answer. Start with the function f(x) = r0 - x², whose derivative is f '(x) = -2x. The Newton approximation formula is given below:
   

   Use x0 = appox(r0) as the initial guess for the formula. After iterating, we will have calculated sqrt(r0) accurate to 16 decimal places.

4. Denormalize: As mentioned above, divide by the square root of the normalizing factor, namely using half the size of the exponent.

Square Root gives Java and C programs to calculate the square root of an arbitrary double r > 0 using normalization as explained above.