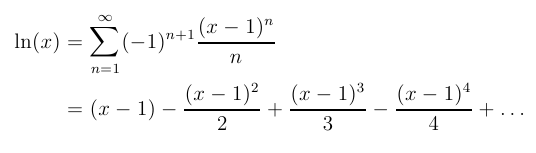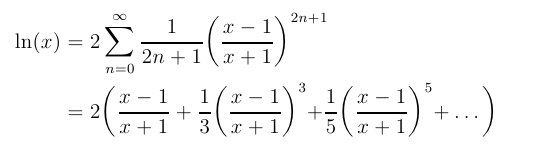Textbook.

CS 3343/3341  Analysis of Algorithms  Calculate: log2(x)

The problem is similar to the work using Newton's Method for square roots: Square Roots, and Newton's Method to find the reciprocal, to perform division: Division. Here we will not be using Newton's Method.

However we will start as with both those cases: using first a normalization step to transform x to x0, where x0 is always located in a fixed interval. Then we will calculate the function of x0, and complete the problem with a denormalization step to get the function applied to the original x. In this part as before, the normalization is multiplication (or a division) by a power of 2, but the denormalization is very different, unexpected.

1. Series Calculation: The key part of calculating log₂x is to use a series. This part will ask you to program one of the series given below.

   Two series are suggested for your use. Each of them converges best for numbers near 1. (The first is a Taylor series for ln(x). The second series is a bit more complicated, but in exchange, it converges much faster for numbers near 1.)

   The series are for ln(x) (the natural logarithm, base e), but the value we want is:

   log₂(x) = (1/ln(2)) * ln(x) = 1.4426950408889634 * ln(x)

   For example,

   log₂(1.25) = (1/ln(2)) * ln(1.25) = 1.4426950408889634 * 0.22314355131420976 = 0.32192809488736235
   log₂(1.3) = (1/ln(2)) * ln(1.3) = 1.4426950408889634 * 0.26236426446749106 = 0.37851162325372983

   So we just need to multiply everything by

   (1/ln(2)) = log₂(e) = 1.4426950408889634
   
   

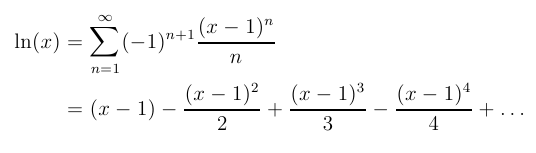
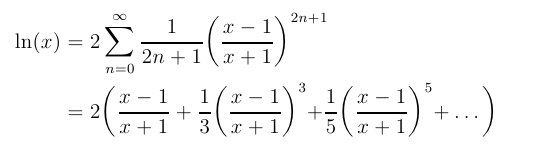   For this part, you should write a program to evaluate one of the two series above for x near 1. The second one is about the same difficulty as the first and is more useful, because of its faster convergence. Test your program with x=5/8=0.625, x=13/20=0.65, x=13/10=1.3, x=3/4=0.75, x=5/4=1.25, and x=3/2=1.5. In order to get 15 digits of accuracy or so, the slower series (first one) will require more terms calculated that the faster series (second one). You should not use an excessive number of terms. [Hint: If you have trouble writing code for this series, you could imitate the similar program in problem 1 above.]

2. Normalization: We want to use an interval with endpoints as close to 1 as possible, because the series converges best for x close to 1. You can normalize into an interval of the form [x/2,x], where you may choose x, which can be a simple value such as 3/2, 5/4, 7/5, 13/10, and in fact any x <= 1.5 and not too close to 1 will work. So suitable intervals would be [3/4,3/2], [5/8,5/4], [7/10,7/5], or [13/20,13/10]. The only answer needed here is to say what interval you are using. (Just choose one.) If you didn't already in part (i) above, you should calculate your series for values at the ends of your interval to see how many terms you will need.

   You must use one of these series to calculate log₂(x) for x in the interval that you choose. This part does not use an approximating function, as the applications involving Newton's method did. The series not only approximates, but calculates directly. However, these series won't work very far away from the interval that you use. That is why we have to normalize in this case also.

3. De-Normalization: After using the series, you must denormalize. The denormalization does not depend on the particular interval that you chose above, but just on the number of times you multiply (or divide) by 2 during normalization. Create a diagram similar to the diagrams we used for square root and division, showing normalization and denormalization. The denormalization may be a surprise to you. (This is by far the most interesting part of this problem.)

   [Here is the diagram:

   

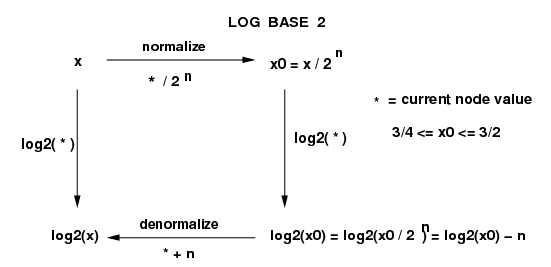   Perhaps most surprising is the * + n denormalizing operation, but we are taking log₂ of the normalizing factor, which is 1/2ⁿ, and this works out to be -n.]

4. Final Results: When you get done, you should have a function that will find log₂(x) correct to 15 digits of accuracy for any input double x. You should try inputs both larger and smaller than your chosen interval, as well as one inside it, such as x=10, x=0.01 and x=1.1.