CS 3343/3341 Introduction to Algorithms Weird Topic |
Fibonacci Matrices,
Part 1 |
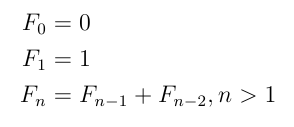
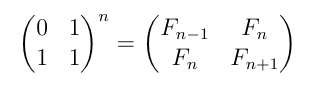
int f(int n) {
if (n <= 1) return n;
return f(n-1) + f(n-2);
}
|
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... |
| An | 1 | 1 | 3 | 5 | 9 | 15 | 25 | 41 | 67 | 109 | 177 | ... |
| A0 = 1 A1 = 1 An = An-1 + An-2 + 1 |
| An = 2 * Fn+1 -1 |
| Recursive calculation of Fn is an exponential algorithm, with performance: |
int f(int n) {
int f0 = 0, f1 = 1, f2 = -1;
for (int i = 1; i < n; i++) {
f2 = f0 + f1;
f0 = f1;
f1 = f2;
}
return f2;
} |
| Standard (looping) calculation of Fn is a linear algorithm, with performance: |
| Fibonacci Matrix calculation of Fn is an unexpected algorithm, with performance: |
| n | φn | {φn} = Ln |
φn/√5 | {φn/√5} = Fn |
|---|---|---|---|---|
| 0 | 1.0 | (1) | 0.4472135954999579 | 0 |
| 1 | 1.618033988749895 | (2) | 0.7236067977499789 | 1 |
| 2 | 2.618033988749895 | 3 | 1.1708203932499368 | 1 |
| 3 | 4.23606797749979 | 4 | 1.8944271909999157 | 2 |
| 4 | 6.854101966249686 | 7 | 3.065247584249853 | 3 |
| 5 | 11.090169943749476 | 11 | 4.959674775249769 | 5 |
| 6 | 17.944271909999163 | 18 | 8.024922359499623 | 8 |
| 7 | 29.03444185374864 | 29 | 12.984597134749393 | 13 |
| 8 | 46.978713763747805 | 47 | 21.009519494249016 | 21 |
| 9 | 76.01315561749645 | 76 | 33.99411662899841 | 34 |
| 10 | 122.99186938124426 | 123 | 55.00363612324743 | 55 |
| 15 | 1364.0007331374366 | 1364 | 609.9996721309716 | 610 |
| 20 | 15126.999933893048 | 15127 | 6765.000029563936 | 6765 |
| 25 | 167761.000005961 | 167761 | 75024.99999733428 | 75025 |
| 30 | 1860497.9999994645 | 1860498 | 832040.0000002412 | 832040 |
| 35 | 20633239.000000075 | 20633239 | 9227464.999999989 | 9227465 |
| 40 | 228826127.0000003 | 228826127 | 102334155.00000013 | 102334155 |