CS 3343/3341
  Introduction to Algorithms  
Weird Topic
  Fibonacci Matrix Programs  

The Fibonacci Numbers consist of the sequence of integers: F0 = 0, F1 = 1, F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, F7 = 13, F8 = 21, F9 = 34, F10 = 55, ... . These are defined recursively by the following formula:

These numbers are also entries of successive powers of the matrix shown below, which can be proven by induction:

The program below uses simple matrix multiplication of 2-by-2 matrices in the C language. A program demonstrating matrix multiplication in Java and C, with and without a matrix as the return value, is here.

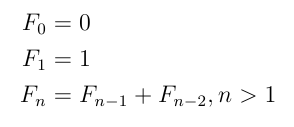
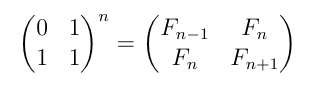
/* Program to take successive powers
   of Fibonacci matrix.
 */
#include <stdio.h>
void printmat(int[2][2]);
void mult(int [2][2], int [2][2],
          int [2][2]);
void copy(int [2][2], int [2][2]);

int main(){
   int a[2][2] = {{0, 1}, {1, 1}};
   int b[2][2], c[2][2];
   int n;
   copy(a, c);
   n = 1;
   while (1) {
      printf("a<sup>%i</sup>, with ", n);
      printf("F<sub>%i</sub>, F<sub>%i</sub>,\
 F<sub>%i</sub>:\n", n-1, n, n+1);
      printmat(c);
      n++;
      if (n >= 15) break;
      copy(c, b);
      mult(a, b, c);
   }
}

void printmat(int x[2][2]){
   int i, j;
   for (i = 0; i < 2; i++){
      printf("|");
      for (j = 0; j < 2; j++)
        printf("%4i ", x[i][j]);
      printf("|\n");
   }
   printf("\n");
}

// z = x*y, mult of 2-by-2 matrices
void mult(int x[2][2], int y[2][2],
          int z[2][2]){
   int i, j, k;
   for (i = 0; i < 2; i++) {  // rows
      for (j = 0; j < 2; j++) {  // cols
         z[i][j] = 0;
         for (k = 0; k < 2; k++)
            z[i][j] += x[i][k] * y[k][j];
      }
   }
}

// y = x, perhaps confusing order
void copy(int x[2][2], int y[2][2]) {
   int i, j;
   for (i = 0; i < 2; i++)  // rows
      for (j = 0; j < 2; j++) // cols
         y[i][j] = x[i][j];
}

% cc -o mat2 mat2.c
% ./mat2
a1, with F0, F1, F2:
|   0    1 |
|   1    1 |

a2, with F1, F2, F3:
|   1    1 |
|   1    2 |

a3, with F2, F3, F4:
|   1    2 |
|   2    3 |

a4, with F3, F4, F5:
|   2    3 |
|   3    5 |

a5, with F4, F5, F6:
|   3    5 |
|   5    8 |

a6, with F5, F6, F7:
|   5    8 |
|   8   13 |

a7, with F6, F7, F8:
|   8   13 |
|  13   21 |

a8, with F7, F8, F9:
|  13   21 |
|  21   34 |

a9, with F8, F9, F10:
|  21   34 |
|  34   55 |

a10, with F9, F10, F11:
|  34   55 |
|  55   89 |

a11, with F10, F11, F12:
|  55   89 |
|  89  144 |

a12, with F11, F12, F13:
|  89  144 |
| 144  233 |

a13, with F12, F13, F14:
| 144  233 |
| 233  377 |

a14, with F13, F14, F15:
| 233  377 |
| 377  610 |

Using repeated squaring one can much more quickly get to larger Fibonacci numbers -- twice a big a number at each step.

/* Program to take successive squares
   of Fibonacci matrix.
   Numbers are as big as a double allows.
 */
#include <stdio.h>
void printmat(double[2][2]);
void mult(double [2][2], double [2][2],
          double [2][2]);
void copy(double [2][2], double [2][2]);

int main(){
   double a[2][2] = {{0.0, 1.0}, {1.0, 1.0}};
   double b[2][2], c[2][2];
   int n, p;
   copy(a, c);
   n = 0; p = 1;
   while (1) {
      printf("a<sup>%i</sup>, with ", p);
      printf("F<sub>%i</sub>, F<sub>%i</sub>,\
 F<sub>%i</sub>:\n", p-1, p, p+1);
      printmat(c);
      n++;
      p *= 2;
      if (n >= 7) break;
      copy(c, b);
      mult(b, b, c);
   }
}

// remainder of this program as above

% cc -o mat3.1 mat3.1.c
% ./mat3.1
a1, with F0, F1, F2:
|   0    1 |
|   1    1 |

a2, with F1, F2, F3:
|   1    1 |
|   1    2 |

a4, with F3, F4, F5:
|   2    3 |
|   3    5 |

a8, with F7, F8, F9:
|  13   21 |
|  21   34 |

a16, with F15, F16, F17:
| 610  987 |
| 987 1597 |

a32, with F31, F32, F33:
|1346269 2178309 |
|2178309 3524578 |

a64, with F63, F64, F65:
| 6557470319842 10610209857723 |
|10610209857723 17167680177565 |

Revision date: 2012-09-17. (Please use ISO 8601, the International Standard Date and Time Notation.)