CS 3343/3341
  Introduction to Algorithms  
Fibonacci Numbers:
Cascade of
Recursive Calls

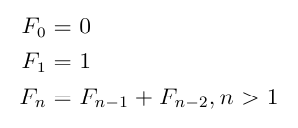
Fibonacci numbers: The Fibonacci numbers are the sequence F0 = 0, F1 = 1, F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, F7 = 13, .... They are defined recursively by:

Here is a short recursive program to calculate them and to measure the elapsed time (not the CPU time):

// Fibonacci: compute Fibonacci numbers
public class Fibonacci { 
   public static long calls = 0;

   public static long f(long n) {
      calls++;
      if (n <= 1) return n;
      return f(n-1) + f(n-2);
   }

   public static void elapsedTime(long startTime) {
      long stopTime = System.currentTimeMillis();
      double elapsedTime = ((double)(stopTime - startTime))/1000.0;
      System.out.println(elapsedTime + " sec." +
         "  " + calls);
   }

   public static void main(String[] args) {
      long startTime = System.currentTimeMillis();
      for (int i = 0; i < 10; i++) {
         calls = 0;
         System.out.println(i + "    " + f(i) +
            "    " + calls);
      }
      System.out.println();
      for (int i = 5; i <= 50; i += 5) {
         calls = 0;
         System.out.print(i + "  " + f(i) + "\t");
         elapsedTime(startTime);
      }
   }
}

With output (slightly edited, with headers inserted by hand):

n  F(n) calls
-------------
0   0       1
1   1       1
2   1       3
3   2       5
4   3       9
5   5      15
6   8      25
7   13     41
8   21     67
9   34    109

 n    F(n)          Elapsed time   Calls
------------------------------------------------
 5  5                  0.002 sec.  15
10  55                 0.005 sec.  177
15  610                0.007 sec.  1973
20  6765               0.007 sec.  21891
25  75025              0.012 sec.  242785
30  832040             0.061 sec.  2692537
35  9227465            0.516 sec.  29860703
40  102334155          5.006 sec.  331160281
45  1134903170        51.297 sec.  3672623805
50  12586269025      573.708 sec.  40730022147
55  139583862445    6436.252 sec.  451702867433
60  1548008755920  69839.095 sec.  5009461563921

Contrast the above recursive calculation of the Fibonacci numbers with the following non-recursive version, whose code is trickier, perhaps a little more error-prone. (This code uses the Java long integer type to get 64-bit integers.)

// Fibonacci0: compute Fibonacci numbers without recursion
public class Fibonacci0 { 

   public static long f(long n) {
      long f0 = 0, f1 = 1, f2 = -1;
      for (long i = 1; i < n; i++) {
         f2 = f0 + f1;
         f0 = f1;
         f1 = f2;
      }
      return f2;
   }

   public static void elapsedTime(long startTime) {
      long stopTime = System.currentTimeMillis();
      double elapsedTime = ((double)(stopTime - startTime))/1000.0;
      System.out.println(elapsedTime + " sec.");
   }

   public static void main(String[] args) {
      long startTime = System.currentTimeMillis();
      for (int i = 2; i < 20; i++)
         System.out.println("n: " + i + "\tF(n): " + f(i));
      System.out.println();
      for (long i = 5; i < 95; i += 5) {
         System.out.print("n: " + i + "\tF(n): " + f(i) + "\t");
         elapsedTime(startTime);
      }
   }
}

The following output (again slightly edited) shows that none of these calculations take any time to speak of. A calculation of the 90th Fibonacci number using the previous method would take at least 10^11 seconds, or over 3000 years, and computer memory would not remotely permit the calculation.

 n  F(n)
--------
 2  1
 3  2
 4  3
 5  5
 6  8
 7  13
 8  21
 9  34
10  55
11  89
12  144
13  233
14  377
15  610
16  987
17  1597
18  2584
19  4181

 n  F(n)                Elapsed time
------------------------------------
 5  5                     0.020 sec.
10  55                    0.032 sec.
15  610                   0.033 sec.
20  6765                  0.033 sec.
25  75025                 0.035 sec.
30  832040                0.035 sec.
35  9227465               0.035 sec.
40  102334155             0.036 sec.
45  1134903170            0.037 sec.
50  12586269025           0.038 sec.
55  139583862445          0.038 sec.
60  1548008755920         0.038 sec.
65  17167680177565        0.040 sec.
70  190392490709135       0.040 sec.
75  2111485077978050      0.040 sec.
80  23416728348467685     0.041 sec.
85  259695496911122585    0.041 sec.
90  2880067194370816120   0.041 sec.

The moral here is important: recursion is a powerful and useful tool that every computer scientist must be familiar with. However, recursion is not always the appropriate method.

Revision date: 2012-08-29. (Please use ISO 8601, the International Standard Date and Time Notation.)