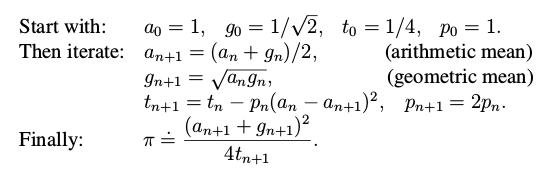| |
Iterative Pi, using the Arithmetic-Geometric mean:
An advanced iterative method to efficiently calculate Pi is given at
the Wikipedia web page:
The algorithm gives slightly more than double the number of digits
with each iteration.
Here is a Python implementation of the algorithm. It requires
a Python arbitrary precision floating point package (mpmath).
|
Arithmetic-geometric Iteration |
|---|
# Pie.py: calculate pi, using arithmetic-geometric mean
# See: en.wikipedia.org/wiki/Gauss-Legendre_algorithm
from mpmath import * # high floating point precision library
# Note: below much is converted to high precision by use
mp.dps = 45 # num of digits for calculations
N = 4 # number of steps
print("Prec: ", mp.dps, ", iters: ", N)
a = mpf(1)
g = 1/sqrt(2)
t = 1/mpf(4)
p = 1
for k in range(1, N+1):
an = (a + g)/2 # arithmetic mean
gn = sqrt(a*g) # geometric mean
tn = t - p*(a - an)**2
pn = 2*p
a, g, t, p = an, gn, tn, pn
print(" ", ((a + g)**2)/(4*t)) # approximate pi
print("\npi:", pi) # exact pi |
Here is a run of the above code:
Pi, correct to 40 digits.
(Bold Correct, Green incorrect) |
$ python3 Pie.py
Prec: 45 , iters: 4
3.141592653589793238462643383279502884197114678
pi:
3.1415926535897932384626433832795028841971694S
1 2 3 4
123456789012345678901234567890123456789012345
|
|
Pi, correct to 83 and 170 digits (separate runs). |
$ python3 Pie2.py
Prec: 85 , iters: 5
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899
862563
pi:
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899
862803
1 2 3 4 5 6 7 8
12345678901234567890123456789012345678901234567890123456789012345678901234567890
$ python3 Pie3.py
Prec: 180 , iters: 6
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899
86280348253421170679821480865132823066470938446095505822317253594081284811174502
8410270193621252485
pi:
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899
86280348253421170679821480865132823066470938446095505822317253594081284811174502
8410270193852110556
1 2 3 4 5 6 7 8
12345678901234567890123456789012345678901234567890123456789012345678901234567890
|
Items of Interest or for study:
Here is a summary of results of the first 13 iterations, the last of which gives
more than 40,000 digits of Pi. Even though 40,000-digit floating point
accuracy is required in the calculations,
only relatively few operation (a hundred or so) are
needed. This method is far faster than others in this writeup.
The 40,000 digits of Pi are obtained on my ancient PC with no noticable
delay.
|
Summary results for successive values of N. |
col 1: the value of N in the program
col 2: actual num of correct digits produced each time
col 3: = 2 times col2: expected correct digits next time
col 4: extra correct digits actually produced next time
(very slightly more than doubling each time)
1 2 4 3
2 7 14 4
3 18 36 4
4 40 80 3 (actual run above)
5 83 166 4 (actual run above)
6 170 340 4 (actual run above)
7 344 688 5
8 693 1386 5
9 1391 2782 5
10 2787 5574 7
11 5581 11162 8
12 11170 22340 7
13 22347 > 40000 A BIT QUICKER THAN DOUBLING
|
History:
In 1853 Willian Shanks calculated 527 correct digits of pi (plus 6
incorrect digits at the end). For the next 20 years he extended
his calculations to 707 digits. During his lifetime he was famous
for this effort, and only long after his death did it come out
that all 20 years worth of digits were incorrect.
In 1961, Shanks (a different one) and Wrench used a powerful IBM 7090
to calculate 100000 correct digits of pi in 8.7 hours, checking the
result by another method.
Just now (2023) I've used my modest 2018 double CPU Dell tower and
the above algorithm to produce 100000 digits of pi (correctness
easily checked online). This took only a fraction of one second
in wall-clock time (including input/output).
More about pi:
See: The Number Pi.
|