CS 3721 Programming Languages   Spring 2014
9. Parse REs, ε-moves
Week 10: Mar 25 - 27

Submit following directions at: submissions and rules at: rules. Deadlines are: 2014-04-04  23:59:59 (that's Fri, 4 Apr 2014, 11:59:59 pm) for full credit. 2014-04-08  23:59:59 (that's Tue,  8 Apr 2014, 11:59:59 pm) for 75% credit.

   M ---> P '$'
   P ---> Q { '|' Q }
   Q ---> R { '+' R }
   R ---> S  '*'  |  S
   S ---> '(' P ')' | '.' | lc

   M ---> P '$'
   P ---> Q { '|' Q }
   Q ---> R { R }
   R ---> S  '*'  |  S
   S ---> '(' P ')' | '.' | lc

The terminal "lc" stands for a lower-case letter, although we could handle many other symbols as well, including upper-case letters, a blank, and other symbols that are not metasymbols: $ | * . ( ) Then with more effort one could fix it up to use backslash (escape) characters for the metasymbols. And so on, with not stopping point.

The three RE operators, from lowest to highest precedence are:

| , the "or" operator,
+ , the "concatenation" operator, and
* , the "star" operator.

In the second part of the problem, we will replace + with nothing at all: concatenation of two REs will be implied by writing one after the other.

---

1. Parser for REs. This should be a recursive-descent parser based on the above grammar. [You could partly imitate the program for the BetterBare parser. Here you should use the explicit '+' operator and the grammar rule that uses this operator.]

   ---

2. Output RPN. Add code to your parser to that it will output the RE in RPN form.

   ---

3. Modify the Parser to Eliminate +. Modify your parser in part 1 so that it will replace the explicit concatenation operator + with nothing, just writing one RE after another. Thus you should use the red grammar rule rather than the one above it. The new version should still output RPN, including an explicit + in the RPN for concatenation. [Hint: this is easy, since some types of terminals are at the start of a RE and other types cannot be at the start of a RE. Your code could the the check either way.]

   What to Turn In: If you complete the program in Problem 3 above you only need the source code for it. Otherwise give the source for the program in Problem 1. Run your program with the last three inputs below, showing the results.

   Test Data:

   Test Data for RE Parser and Translator to RPN
   RE, With '+'	RE, Without '+'	RPN form
   (a+b)*$	(ab)*$	ab+*$
   (a|b)*+a+b+b$	(a|b)*abb$	ab|*a+b+b+$
   a*+b*+c*$	a*b*c*$	a*b*+c*+$
   .*+(a+b|a+a+c)$	.*(ab|aac)$	(not supplied)
   .*+(a+b|a+c)+(a+b|a+c)*+d$	.*(ab|ac)(ab|ac)*d$	(not supplied)
   (a|b)*+(a+a|b+b)+(a|b)*$	(a|b)*(aa|bb)(a|b)*$	(not supplied)

4. Consider the NFA that below that is used to recognize the language of the regular expression /.*(ab|aac)/. Here we're only interested in the first two steps of the subset algorithm applied by hand to this NFA, as part of the process of converting this NFA into a DFA, by hand. [It is possible to greatly simplify this NFA, but you are not to do this. This is an exercise about the ε-closure algorithm.]
   
   1. Notice that the start state of the NFA is 2. The start state for the corresponding DFA won't be {2}, but will be ε-closure({2}). You are to apply the ε-closure algorithm to {2} step-by-step, showing at each stage states pushed on the stack and showing states as they are colored black. (The collection of all black states is the ε-closure.) [Hint: there are 6 states in this closure.]

   2. Next, assume that the first input character is an "a". You are to calculate the result of following arrows labeled with "a" or with "." from states in closure({2}) to other states and making a set of these states. [Answer: {1,5,9}.]

   3. Finally, calculate ε-closure({1,5,9}) and show the calculation step-by-step as in the first item above.

5. Use the extended subset algorithm to find the DFA that corresponds to the following NFA:
   

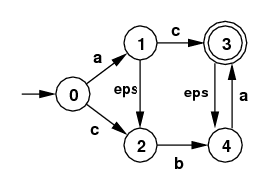
6. Suppose you want to handle the regular expression: /ab(ab)*/. The figure below gives this converted to an NFA with ε-moves. (Here "@" is what I use for ε in programs (ε = the empty string). This isn't the only NFA that will work, but this is the one you must work with. Below, the transition from state 7 to state 9 should be labeled with @.)
   
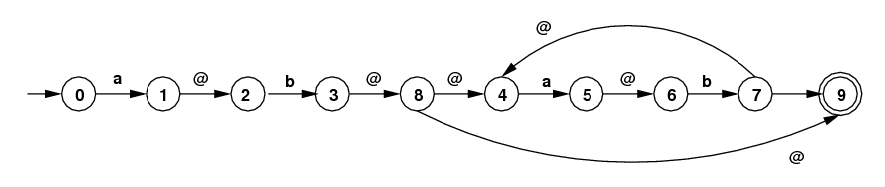
   1. Carry out the extended subset algorithm on this NFA to get a DFA that accepts the same language. [Your answer should have 6 states including the empty set as an error state.]

   2. This DFA is not optimal: it doesn't have the minimal number of states. But it can be converted to that optimal DFA by identifying two pairs of its states: the two terminal states (there are only 2), and two of the non-terminals. See if you can figure out what the minimal DFA is. (You haven't been given an algorithm for this.)