|
CS 3721 Programming Languages Spring 2014 | |
9. Parse REs, ε-moves
| ||
Possible Answers in Red
| ||
Grammar for REs: Here is a grammar for our simplified regular expressions that is appropriate for the work in this course and is designed for a recursive-descent parser:
| Grammar: Regular Expressions | |
|---|---|
| With explicit '+' | Without explicit '+' |
M ---> P '$'
P ---> Q { '|' Q }
Q ---> R { '+' R }
R ---> S '*' | S
S ---> '(' P ')' | '.' | lc
| M ---> P '$'
P ---> Q { '|' Q }
Q ---> R { R }
R ---> S '*' | S
S ---> '(' P ')' | '.' | lc
|
-
| , the "or" operator,
+ , the "concatenation" operator, and
* , the "star" operator.
Parser for REs and Translator to RPN:
- Parser for REs. This should be a recursive-descent
parser based on the above grammar. [You could partly imitate the
program for the
BetterBare parser.
Here you should use the explicit '+' operator and the grammar
rule that uses this operator.]
- Output RPN. Add code to your parser to that it will
output the RE in RPN form.
- Modify the Parser to Eliminate +.
Modify your parser in part 1 so that it will replace the
explicit concatenation operator + with nothing, just writing
one RE after another. Thus you should use the red grammar rule
rather than the one above it. The new version should still output RPN,
including an explicit + in the RPN for concatenation.
[Hint: this is easy, since some types of terminals are
at the start of a RE and other types cannot be at
the start of a RE. Your code could the the check either way.]
What to Turn In: If you complete the program in Problem 3 above
you only need the source code for it. Otherwise give the source
for the program in Problem 1. Run your program with the last
three inputs below, showing the results.
Test Data:
Test Data for RE Parser and Translator to RPN RE, With '+' RE, Without '+' RPN form (a+b)*$ (ab)*$ ab+*$ (a|b)*+a+b+b$ (a|b)*abb$ ab|*a+b+b+$ a*+b*+c*$ a*b*c*$ a*b*+c*+$ .*+(a+b|a+a+c)$ .*(ab|aac)$ (not supplied) .*+(a+b|a+c)+(a+b|a+c)*+d$ .*(ab|ac)(ab|ac)*d$ (not supplied) (a|b)*+(a+a|b+b)+(a|b)*$ (a|b)*(aa|bb)(a|b)*$ (not supplied)
ε-closure algorithm Read the page NFAs with ε-moves. You need to understand the ε-closure algorithm.
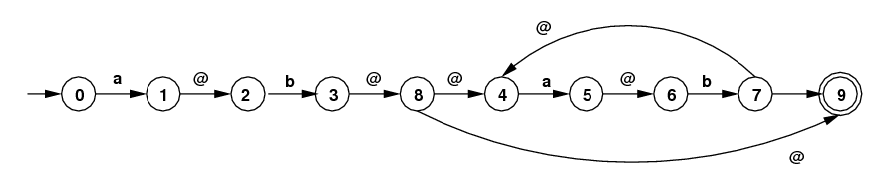
- Consider the NFA that below that is used to recognize
the language of the regular expression
/.*(ab|aac)/. Here we're only
interested in the first two steps of the subset algorithm
applied by hand to this NFA, as part of the process of
converting this NFA into a DFA, by hand.
[It is possible to greatly simplify this NFA, but you
are not to do this. This is an exercise about the
ε-closure algorithm.]

- Notice that the start state of the NFA is 2. The start state for the corresponding DFA won't be {2}, but will be ε-closure({2}). You are to apply the ε-closure algorithm to {2} step-by-step, showing at each stage states pushed on the stack and showing states as they are colored black. (The collection of all black states is the ε-closure.) [Hint: there are 6 states in this closure.]
- Next, assume that the first input character is an "a". You are to calculate the result of following arrows labeled with "a" or with "." from states in closure({2}) to other states and making a set of these states. [Answer: {1,5,9}.]
- Finally, calculate ε-closure({1,5,9}) and show the calculation step-by-step as in the first item above.
Below, each pop is the start of another iteration of the while loop.Recitation 9 4.a) @-closure({2}), 4.b) 4.c) @-closure({1, 5, 9}) 4.a) @-closure({2}) color 2 black (P) push 2, Stack: 2 pop 2 follow 2 to 0 color 0 black push 0, Stack: 0 follow 2 to 3 color 3 black push 3, Stack: 0, 3 pop 0 (do nothing) pop 3 follow 3 to 14 color 14 black push 14, Stack: 14 pop 14 follow 14 to 4 color 4 black push 4, Stack: 4 follow 14 to 8 color 8 black push 8, Stack: 4, 8 pop 4 (do nothing) pop 8 (do nothing) Stack: empty Result: {2, 0, 3, 14, 4, 8}
4.b) {1, 5, 9} @ . 2 ---> 0 ---> 1 @ @ @ a 2 ---> 3 ---> 14 ---> 4 ---> 5 @ @ @ a 2 ---> 3 ---> 14 ---> 8 ---> 94.c) @-closure({1, 5, 9}) color 1 black color 5 black color 9 black push 9, 5, 1, Stack: 1, 5, 9 pop 1 follow 1 to color 0 black push 0. Stack: 3, 0, 5, 9 follow 1 to 3 color 3 black push 3 pop 0 (do nothing) [not in order] pop 3 follow 3 to 14 color 14 black push 14. Stack: 14, 5, 9 pop 14 follow 14 to 4 color 4 black push 4. Stack: 4, 5, 9 follow 14 to 8 color 8 black push 8. Stack: 8, 4, 5, 9 pop 4 (do nothing) pop 8 (do nothing) pop 5 follow 5 to 6 color 6 black push 6. Stack: 6, 9 pop 6 (do nothing) pop 9 follow 9 to 10 color 10 black push 10. Stack: 10 pop 10 (do nothing) Stack: empty Result: {1, 5, 9, 0, 3, 14, 4, 8, 6, 10}
Subset Algorithm With ε-moves: See NFAs with ε-moves. Notice that the only difference between this and the former subset algorithm (the one that didn't allow ε-moves) is: Here we compulsively take the ε-closure of each subset generated.
- Use the extended subset algorithm to find the DFA that
corresponds to the following NFA:
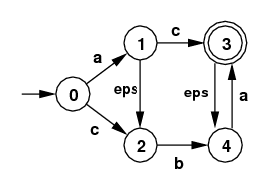
State a b c S 0 {0} 1 {1,2} 2 {} 3 {2} 1 {1,2} 2 {} 4 {4} 5 {3,4} 2 {} 2 {} 2 {} 2 {} 3 {2} 2 {} 4 {4} 2 {} 4 {4} 5 {3,4} 2 {} 2 {} T 5 {3,4} 5 {3,4} 2 {} 2 {} 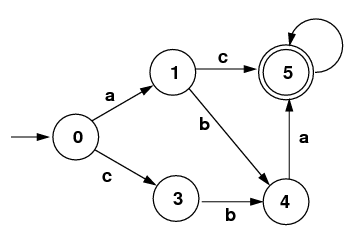
-
Suppose you want to handle the regular expression:
/ab(ab)*/.
The figure below gives this converted to an
NFA with ε-moves.
(Here "@" is what I use for ε in programs
(ε = the empty string).
This isn't the only NFA that will work, but this is the one
you must work with. Below, the transition from state
7 to state 9 should be labeled with @.)
- Carry out the extended subset algorithm on this NFA to get a DFA that accepts the same language. [Your answer should have 6 states including the empty set as an error state.] The DFA table is below on the left.
- This DFA is not optimal: it doesn't have the minimal number of states. But it can be converted to that optimal DFA by identifying two pairs of its states: the two terminal states (there are only 2), and two of the non-terminals. See if you can figure out what the minimal DFA is. (You haven't been given an algorithm for this.) Diagrams are below at the right.
State a b S 0 {0} 1 {1,2} 2 {} 1 {1,2} 2 {} 3 {3,4,8,9} 2 {} 2 {} 2 {} T 3 {3,4,8,9} 4 {5,6} 2 {} 4 {5,6} 2 {} 5 {4,7,9} T 5 {4,7,9} 4 {5,6} 2 {} 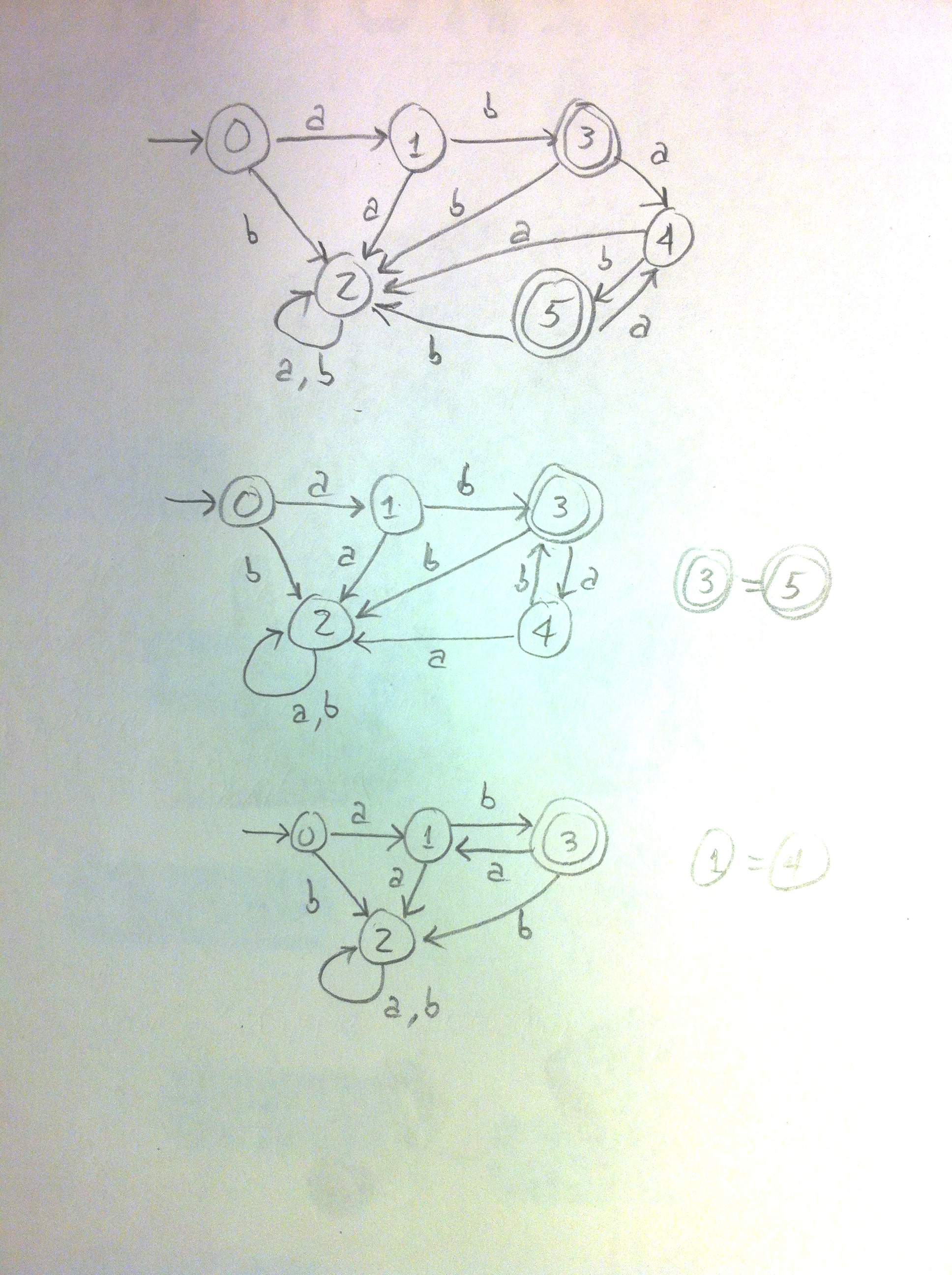
Revision date: 2014-03-24. (Please use ISO 8601, the International Standard.)
