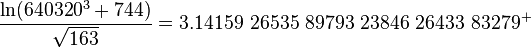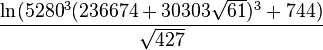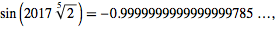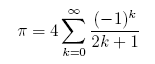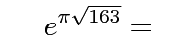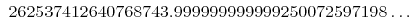| |
 |
|
CS 3723
Programming Languages |
13. Arbitrary-Precision Float
|
|
Support for Arbitrary-Precision:
Python lets ints be arbitrarily large (subject to available memory).
Ordinary Python can't handle floating point numbers with more significant
digits than a double (about 16), so if you want higher precision,
you need some other software:
- mpmath:
a third-party addition to Python, this seems the best choice.
- I installed it on my Linux system (using Python 2.6.5) at home
with no trouble, downloading it from the link above and following
directions at that link (to install you just run a Python program).
The package works
for Python 2.5 or higher, including Python 3.x.
My install required root privileges,
so I cannot install it on an elk, but I'll see if
the systems people will do that.
- I also installed it on a Mac computer,
running OSX 10.6.8 (Leopard) with Python 2.6.1.
This install was just as easy, again using root access. (Root access is
disabled on Macs by default, but online Apple support tells how to
enable it.)
- It is also available for Windows, but I couldn't try that.
(No Windows!)
It is pure-Python code, and seems very sophisticated, with
a lot of fancy capabilities and features. I'm just getting started
on this (see below). See also mpmath docs.
I tested both the Linux and the Mac OSX versions.
Here is the tar file that contains the software:
mpmath-0.19.tar.
To extract the software, download and type:
tar xf mpmath-0.19.tar
- Others:
Python has other such arbitrary-precision float libraries,
as do C and Lisp and many others.
Sample Calculations:
Here are computations of three formulas.
The first is a famous weird formula that's very close to an integer:
|
mpmath: Sample Calculations |
|---|
# mpmath_test.py
from mpmath import *
import sys
mp.dps = 50 # 50 digit calculations
print "Precision: ", mp.dps
print mpf(2)**mpf('0.5') # sqrt(2)
print 2*pi # 2*pi
near_int = e**(pi*mpf(163)**mpf('0.5'))
print near_int # very close to an int
| % Python mpmath.py
Precision: 50
1.4142135623730950488016887242096980785696718753769
6.2831853071795864769252867665590057683943387987502
262537412640768743.99999999999925007259719818568887
1 2 3 4 5
12345678901234567890123456789012345678901234567890
(all digits above are correct)
|
Next are two formulas giving π accurate to 30 and
to 52 decimals.
|
mpmath: More Sample Calculations |
|---|
# tmp.py
from mpmath import *
import sys
mp.dps = 80
print "Precision: ", mp.dps
pi_approx = mp.log(mpf(640320) ** 3 + mpf(744)) / mp.sqrt(163)
print pi_approx
pi_approx2 = mp.log( (mpf(5280) * (mpf(236674) + mpf(30303) * \
mp.sqrt(mpf(61)))) ** 3 + mpf(744)) / mp.sqrt(mpf(427))
print pi_approx2
print pi
|
% Python tmp.py
Precision: 80
3.1415926535897932384626433832797266193475498808835224222929628774422587390510494
3.1415926535897932384626433832795028841971693993751058600689073618724169264129391
3.141592653589793238462643383279502884197169399375105820974944592307816406286209
1 2 3 4 5 6 7 8
12345678901234567890123456789012345678901234567890123456789012345678901234567890
|
Try this one:
Items of Interest or for study
(see mpmath docs):
- You can use import mpmath at the head, but then you
need to add mpmath. at the start of the references to the library.
- mp.dps=50 declares the precision to be 50 digits.
You can change this precision any time in the program.
- mpf(2) declares a high-precision constant with value 2.
Notice from the mpmath docs
that mpr(10.1) doesn't work correctly, while
mpr('10.1') does.
- The software works with ordinary arithmetic operators and
with ordinary integer constants. (I've sometimes changed
an integer constant to multi-precision form when it wasn't required.)
- There are often alternatives to ordinary operators, as with:
| Instead of ... |
you can write: |
| e ** (...) | mp.exp(...) |
| (...) ** mpf('0.5') | mp.sqrt(...) |
- Determining error bounds is important and hard to do.
I haven't been bothering with this, and I'm sticking to problems
where I already know the correct answer.
Gregory's Series:
Here we're showing a larger calculation: sums of Gregory's series,
using the formula below. These sums are computed with up to 130-digit
accuracy, using Python, with the mpmath extension. (I've carried
out many of these calculations on Mathematica and clisp,
getting exactly the same results.)
|
mpmath: More Sample Calculations |
|---|
| Ordinary Python |
Python with mpmath |
|---|
# greg.py
import sys
N = 100000
sum = 0.0
sign = 1
for k in range(0,N):
term = 1.0/(2.0*k + 1.0)
sum = sum + sign*term
if k%(N/50) == 0:
sys.stdout.write(str(k) +
" " + str(sum) + "\n")
sign = -sign
sys.stdout.write(str(k) + " " +
str(sum) + "\n")
sys.stdout.write(str(k) +
" " + str(sum*4) + "\n")
|
# greg_mp.py: sum Gregory's series, multi-prec
from mpmath import *
import sys
mp.dps = 100
print "Precision: ", mp.dps
N = 10000000
sum = mpf(0)
sign = 1
for k in range(0,N):
term = mpf(1)/(mpf(2)*k + (mpf(1)))
sum = sum + sign*term
if k%(N/50) == 0:
sys.stdout.write(str(k) + " " +
str(sum) + "\n")
sign = -sign
sys.stdout.write(str(k) + " " +
str(sum) + "\n")
sys.stdout.write(str(k) + " " +
str(sum*4) + "\n")
|
Below, the blue digits are initial correct ones,
the red digits are incorrect,
and the green digits are
correct digits that come after at least one incorrect one.
|