|
CS 3723 Programming Languages Fall 2014 | |
Homework 11. Python Classes
| ||
Week 14-15: Nov 24 - Dec 5
| ||
Submit following directions at:
submissions
and rules at:
rules.
Deadlines are:
|
- Main reference:
O-O Programming in Python: Defining Classes.
- Earlier section that can be useful: Review of Basic Python.
| Class Implementing Fractions | Rest + Output |
|---|---|
# fraction.py: implement fractions
import sys
# num = top = numerator
# den = bottom = denominator
def gcd(m,n): # m can be negative
while m%n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
class Fraction:
def __init__(self,top,bottom):
self.num = top
self.den = bottom
sys.stdout.write("New: ")
Fraction.show(self)
sys.stdout.write("\n")
def __str__(self):
return str(self.num)+"/"+str(self.den)
def show(self):
sys.stdout.write(str(self.num) + "/" +
str(self.den))
def __add__(self,other):
newnum = self.num*other.den + \
self.den*other.num
newden = self.den * other.den
com = gcd(newnum,newden)
return Fraction(newnum//com,newden//com)
def __eq__(self, other):
firstnum = self.num * other.den
secondnum = other.num * self.den
return firstnum == secondnum
| u = Fraction(1, 2)
v = Fraction(2, 3)
w = Fraction(3, 7)
x = Fraction(-4, 11)
y = Fraction(-7, 13)
z = Fraction(-2, 5)
sys.stdout.write("u + v: " +
str(u+v) + "\n")
sys.stdout.write("u == v: "+
str(x == y) + "\n")
sys.stdout.write("w + x: " +
str(w+x) + "\n")
sys.stdout.write("u + y: " +
str(u+y) + "\n")
sys.stdout.write("x + y: " +
str(x+y) + "\n")
sys.stdout.write("x: " +
str(x) + "\n")
x = w
sys.stdout.write("x: " +
str(x) + "\n")
|
- Implement the simple methods getNum and getDen that will return the numerator and denominator of a fraction.
- Add functions to handle the other binary infix arithmetic
operators: −,
*, and
/.
These must be functions __sub__, __mul__, and __div__, similar to __add__ above. - Add functions for binary infix comparison operators: !=, <, <=, >, >=. These must be functions __ne__, __lt__, __le__, __gt__, __ge__, similar to __eq__ above.
- "In many ways it would be better if all fractions were maintained in lowest terms right from the start. Modify the constructor for the Fraction class so that gcd is used to reduce fractions immediately. Notice that this means the __add__ function no longer needs to reduce. Make the necessary modifications." (Taken from the link above.)
- Test Code A: This assumes it is included in the same file with the class.
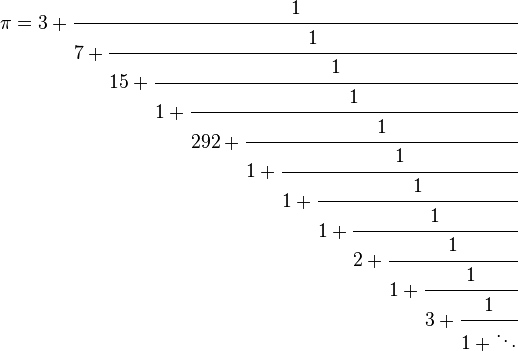First truncation: 3+1/(7+1/(15+1))