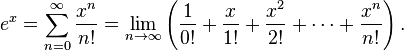| |
 |
|
CS 3723
Programming Languages |
Python Complex Class
|
|
Here is the Complex class from the
final exam
with a few extra features:
methods for the conjugate: conj(a + bj) = (a - bj),
absolute value squared: abs_sq(a + bj) = a^2 + b^2,
and absolute value: abs(a + bj) = √(a^2 + b^2).
I also tried out making the data members private and using the same names
for getReal and getImag as the original data members.
| Complex
Class in Python, constructed "from scratch" |
|---|
# complex.py: complex numbers "from scratch"
# Builtin complex never uses cap C
import math
class Complex(object):
def __init__(self,real,imag=0):
self.__real = float(real)
self.__imag = float(imag)
def __str__(self):
return "(%.8g+%.8gj)" % \
(self.__real, self.__imag)
def __add__(self,other):
return Complex(self.__real + other.__real,
self.__imag + other.__imag)
def __sub__(self,other):
return Complex(self.__real - other.__real,
self.__imag - other.__imag)
def __mul__(self,other):
return Complex(self.__real * other.__real -
self.__imag * other.__imag,
self.__real * other.__imag +
self.__imag * other.__real)
def __div__(self,other):
denom = other.__real **2 + other.__imag **2
if denom == 0:
return None
return Complex((self.__real * other.__real +
self.__imag * other.__imag)/denom,
(self.__imag * other.__real -
self.__real * other.__imag)/denom)
def __eq__(self,other):
return self.__real == other.__real and \
self.__imag == other.__imag
def real(self):
return self.__real
def imag(self):
return self.__imag
def conj(self):
return Complex(self.__real, -self.__imag)
def abs_squared(self):
return self.__real **2 + self.__imag**2
def abs(self):
return math.sqrt(self.abs_squared())
| # test_complex.py: series for exp
import sys, math, cmath
from complex import Complex
def test_loop1(): # 8 multiplications
r = Complex(1.0,1.0)
r16 = Complex(16.0, 0.0)
p = Complex(1.0, 0.0)
print p
for i in range(0,8):
p = p*r
sys.stdout.write(str(p) + " " +
str(p == r16) + '\n')
def test_loop2(): # 8 divisions
r = Complex(1.0,1.0)
r16th = Complex(0.0625, 0.0)
p = Complex(1.0, 0.0)
print p
for i in range(0,8):
p = p/r
sys.stdout.write(str(p) + " " +
str(p == r16th) + '\n')
def test_8th_root_of_1(): # back to 1.0
r2 = math.sqrt(2.0)/2.0
r = Complex(r2,r2)
p = Complex(1.0, 0.0)
print p
for i in range(0,8):
p = p*r
sys.stdout.write(str(p) + '\n')
def cexp(x): # complex series for exp
term = Complex(1.0)
sum = term
for i in range(1,28):
term = term*x*Complex(1.0/float(i))
sum = sum + term
if i < 10:
sys.stdout.write(" ")
sys.stdout.write(str(i)+": " +
str(sum)+'\n')
return sum
sys.stdout.write("\nTest 8 mults\n")
test_loop1()
sys.stdout.write("\nTest 8 divisions\n")
test_loop2()
sys.stdout.write("\nTest 8 mults to 1.0\n")
test_8th_root_of_1()
sys.stdout.write("\nTest series for exp\n")
ipi = Complex(0.0, math.pi)
sys.stdout.write("e^ipi: " +
str(cexp(ipi))+'\n')
sys.stdout.write("\nTest Python's exp\n")
pij = 0+cmath.pi*1j
sys.stdout.write("cmath.exp(0+cmath.pi*1j):"
+ str(cmath.exp(pij)) + '\n')
|
This Complex class would have allowed a good project similar to
the Fraction class that we did. The Swiss mathematician
Leonhard Euler
discovered the formula: 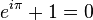 ,
as well as the infinite series for calculating the exponential
function:
This series converges for all x, in particular for
x = 0 + πj (in Python's notation). I would have had you calculate the sum of
the first 25 terms of this series as complex numbers. The program
above carries out this computation, and the series does indeed converge
to 1+0j. Notice that we are not using
Python's built-in complex numbers. ,
as well as the infinite series for calculating the exponential
function:
This series converges for all x, in particular for
x = 0 + πj (in Python's notation). I would have had you calculate the sum of
the first 25 terms of this series as complex numbers. The program
above carries out this computation, and the series does indeed converge
to 1+0j. Notice that we are not using
Python's built-in complex numbers.
| Output of
the program above |
|---|
% python test_complex.py
Test 8 mults
(1+0j)
(1+1j) False
(0+2j) False
(-2+2j) False
(-4+0j) False
(-4+-4j) False
(0+-8j) False
(8+-8j) False
(16+0j) True
Test 8 divisions
(1+0j)
(0.5+-0.5j) False
(0+-0.5j) False
(-0.25+-0.25j) False
(-0.25+0j) False
(-0.125+0.125j) False
(0+0.125j) False
(0.0625+0.0625j) False
(0.0625+0j) True
Test 8 mults to 1.0
(1+0j)
(0.70710678+0.70710678j)
(0+1j)
(-0.70710678+0.70710678j)
(-1+0j)
(-0.70710678+-0.70710678j)
(0+-1j)
(0.70710678+-0.70710678j)
(1+0j)
|
Test series for exp
ipi: (0+3.141592653589793j)
1, (1+3.141592653589793j)
2, (-3.934802200544679+ 3.141592653589793j)
3, (-3.934802200544679+ -2.026120126460176j)
4, ( 0.1239099258720886+-2.026120126460176j)
5, ( 0.1239099258720886+ 0.5240439134171688j)
6, (-1.211352842982501+ 0.5240439134171688j)
7, (-1.211352842982501+ -0.07522061590362306j)
8, (-0.9760222126236076+-0.07522061590362306j)
9, (-0.9760222126236076+ 0.006925270707505135j)
10, (-1.001829104013622+ 0.006925270707505135j)
11, (-1.001829104013622+ -0.000445160238209211j)
12, (-0.9998995297042177+-0.000445160238209211j)
13, (-0.9998995297042177+ 2.114256755840119e-05j)
14, (-1.000004167809142+ 2.114256755840119e-05j)
15, (-1.000004167809142+ -7.727858894290057e-07j)
16, (-0.9999998647395555+-7.727858894290057e-07j)
17, (-0.9999998647395555+ 2.241951071854486e-08j)
18, (-1.00000000352908+ 2.241951071854486e-08j)
19, (-1.00000000352908+ -5.289182787249905e-10j)
20, (-0.9999999999243493+-5.289182787249905e-10j)
21, (-0.9999999999243493+ 1.034818753582179e-11j)
22, (-1.000000000001356+ 1.034818753582179e-11j)
23, (-1.000000000001356+ -1.702841811102599e-13j)
24, (-0.9999999999999796+-1.702841811102599e-13j)
25, (-0.9999999999999796+ 2.737743473350955e-15j)
26, (-1 + 2.737743473350955e-15j)
27, (-1 + 3.051822933575691e-16j)
e^iπ:(-1 + 3.051822933575691e-16j)
cmath.exp(0+cmath.pi*1j): (-1+1.22460635382e-16j)
|
The computation above is converging to -1 plus
an extremely small number times j. The last line on the right above
shows the same calculation using Python's built-in complex
numbers. The two extremely small multiples of
j are different in the two computations, but this is of
no significance (a pun).
Finally the numbers below show the output of the same
computaton, carried to high precision, using the library mpmath.
| Arbitrary Precision
Complex Numbers in Python, using mpmath library |
|---|
% python complex_mpmath.py
(0.0 + 3.141592653589793238462643383279502884197j)
5: ( 0.1239099258720889087677683620913040677485 + 0.5240439134171686530727684557912337378288j)
10: (-1.001829104013621442578255362236712553235 + 0.006925270707504804983831437768892036621276j)
15: (-1.000004167809142365237470033401378834922 - 0.0000007727858897634448344079259855673249670672j)
20: (-0.9999999999243491569656829463991101443086 - 0.0000000005289186131634290398091717071376516464896j)
25: (-0.9999999999999793635436587388265668563339 + 2.403305035355747041912550309652197855868e-15j)
30: (-1.000000000000000000030536341988518572233 + 3.108707909073023766021815358391073476033e-19j)
35: (-1.000000000000000000000002107755552885457 - 1.79029219970697302499873293037084385004e-25j)
40: (-0.9999999999999999999999999999994625280236 - 7.183693811264135340256222537220808666116e-30j)
45: (-0.9999999999999999999999999999999999866208 + 8.944603736934812058552449165710983774179e-37j)
50: (-1.0 + 2.242118931431719972951701196207462110809e-41j)
|
(Revision date: 2014-12-19.
Please use ISO 8601,
the International Standard.)
|

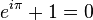 ,
as well as the infinite series for calculating the exponential
function:
,
as well as the infinite series for calculating the exponential
function: