| |
- Give the MIPS assembly program that this Python program will
print. [This MIPS program is error-free. Because this is such a
simple case, I was able to leave off several parts that we have
normally included.]
- How have we been running the MIPS programs that we generate?
- If this MIPS program is run, what will it do? Will it output anything?
[In addition to the standard stuff that's always printed.]
[a): above, b) spim, c) the offset 8 gives
the location of the double 1.0, so it prints 1
or 1.0 after the standard stuff. In the MIPS program, I could
leave off the part that saves and restores $ra because
this program didn't use $ra.]
- (15) MIPS assembly language,
as used in our Tiny compiler:
- Using the way we declared data and memory in the Tiny compiler project,
give a MIPS instruction that will load the double 6.0
into the register $f2. [Do not give the data and memory
declarations.]
[ l.d $f2, 48($s1).
Note: the double 6.0 is located at offset 6*8=48.]
- Again as above, give a MIPS instruction that will store a
double from register $f2 into the location used for the
variable c.
[ s.d $f2, 96($s1).
Note: the variable a is located at offset 80, so
c is at 80+16=96.]
- Parts a) and b) above together form the translation of
a statement in the Tiny language. What is this statement?
[ c=6; ]
- (15) Grammar for Tiny: Consider
the grammar rule from the grammar for the Tiny language:
I ---> '[' E '?' S { S } ':' S { S } ']' | '[' E '?' S { S } ']'
|
- What construct in the Tiny language is this the rule for?
[This is the if-then or
if-then-else ]
- Give two simple Tiny statements that separately match the
two alternatives in the rule. [These should be syntactically correct,
but they don't need to do anything sensible. Variables don't have
to already have values, etc.]
[Almost anything would work:
[ m-n ? a=a-1; : a=a+1; ] or
[ m-n ? < a ; ] ]
- If you also wanted to allow any one or more of the "blocks" described
by the above grammar to be empty (have no statements in them), how
would you change this grammar rule?
[ Replace each S { S } with { S }, that is
zero or more repetitions of S instead or one or more.]
- (20) Translating Tiny Assignment:
Consider the assignment statement with grammar rule:
A --> lower-case '=' E ';'
|
This rule was normally handled by a Python function A( ).
- What data comes into this function that is used for the translation?
[The specific lower-case letter, and address
returned by a call to E..]
- What value is returned, if any?
[The function should return nothing. In Python it
could return anything as long as the returned item was ignored.]
- Write code for the function in as good a detail as you can.
Include code to output the MIPS statement or statements that the function
should produce. [You can assume that you are working with your
own program in terms of whether you've already scanned, etc.
Call whatever "helper" functions you need, without giving their code,
but not a helper function that does all the output.]
[Here's code adapted from my compiler (I used a
separate function that wrote the actual code):addr = {'a':10,'b':11,'c':12,'d':13,'e':14,
'f':15,'g':16,'h':17,'i':18,'j':19,
'k':20,'l':21,'m':22,'n':23,'o':24,
'p':25,'q':26,'r':27,'s':28,'t':29,
'u':30,'v':31,'w':32,'x':33,'y':34,
'z':35}
def A(): # assignment
# called because starts with lower-case
lhs = addr[next]
scan()
if next != '=':
error(5)
else:
scan()
res = E()
if next != ';':
error(6)
scan()
# gen_assign(lhs, res);
gen(" l.d $f2, " + str(8*res) + "($s1)\n")
gen(" s.d $f2, " + str(8*lhs) + "($s1)\n")
Using a dictionary as I did may be the simplest way to get the
offsets, but there are shorter ways. Of course I didn't expect
students to write out an entire dictionary.]
- (20) Translating Tiny +:
Consider the grammar rule that handles a '+' operator:
|
At the right is a function E( ), a simplified version of the
one in my compiler, with the '-' and the output statements left off.
Fill in output statements that print the necessary MIPS
instructions. Add anything else that is needed.
Be sure to show what is returned. [If you use a separate function
to output the MIPS instructions, then also give the code for that function.]
| |
def E():
res = T()
while next == '+':
arg1 = res
scan()
arg2 = T()
res = ...
return res
|
|
[Here's code adapted from my compiler. I used a
separate function that wrote the actual code. I also multiplied
by 8 at the last moment. Instead of my next_var(), I was
recommending that students have a function that returns 288
the first time, and 8 bigger each subsequent time:def E(): # expression
res = T()
while next == '+': # or next == '-'
save = next
arg1 = res
scan()
arg2 = T()
res = 36 + int(next_var())
# gen_op(res, arg1, save, arg2)
gen(" l.d $f2, " + str(8*arg1) + "($s1)\n")
gen(" l.d $f4, " + str(8*arg2) + "($s1)\n")
gen(" add.d $f6, $f2, $f4\n")
gen(" s.d $f6, " + str(8*res) + "($s1)\n")
return res
]
- (10) Changing the Tiny compiler:
Suppose we wanted to convert our Tiny compiler from one
that handled doubles to one that handled 32-bit integers.
(Thus there would be no doubles at all.)
- Would you expect any of the sample programs to still
produce the same output?
[Sure. A number of the programs were integer-only
and should run fine assuming everything was converted to integer,
including the items below and others.]
- What kinds of changes would be needed? (General types of
changes. Give at least three types. Of course you would need
to look up the details to make it all work.)
[Items:
- All storage is multiples of 4 instead of multiples of 8.
This includes integers, storage of lower-case identifiers,
and temporary storage. We would be going from 64-bit doubles
to 32-bit integers.
- Because of the above, the data declarations (after .data)
would be quite different. We would be creating 10 integer
constants: 0, 1, 2, ..., 9. It could look like:
gen(" .data");
gen("M: .word 0,1,2,3,4,5,6,7,8,9 # constants");
gen(" .space 104 # variables a to z");
gen(" .space 500 # temporaries");
- We would be using no double registers, so no $f0 - $f30,
but integer registers instead: $t0, $t1, ..., $s1, $s2, ....
- MIPS I/O is different, but it just uses different values in
$v0, and int registers in place of float ones.
- Many of our current instructions are double only, and need
to be converted to the corresponding integer instruction.
- l.d, s.d would become lw, sw
- add.d, sub.d, mul.d, div.d would become add, sub, mul, div
- MIPS conditional branches are different for integers (and simpler)
- use integer branches: beq, bne, blt, bgt, bge, ble.
These work directly off two registers and so are simpler.
- The framework would be the same except for that after
the .data.
In spite of the list above, this would all be done in a hour of so.
The main problem is researching the proper replacements.
In fact, I did the opposite: I converted the project from 32-bit integers
to doubles. This is the harder direction, but it was still fairly
easy.]
- (20) Python classes, complex numbers:
[Python already supports complex numbers, just as it supports
fractions, but as with fractions, we can write a complex
number class from scratch. You don't have to understand
complex numbers in order to complete this problem. Just know that a
complex number is a pair of real numbers: a real part
and an imaginary part, with funny ways to add, subtract, multiply,
and divide them. A number with real part 2 and
imaginary part 3 is often written 2+3j, where j
is the infamous square root of −1; more often
i is used in place of j. Of course there are complex
number deniers, who especially deny the existence of
imaginary numbers -- why else did they call them "imaginary"?]
We can perform the operations +, −, *, /, and == on complex numbers
as follows:
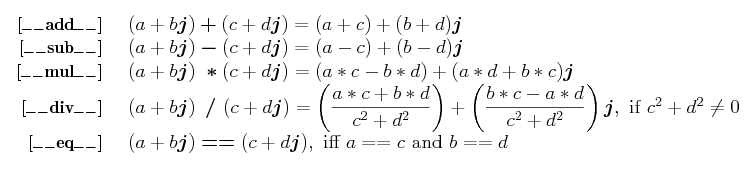
Above on the left in each case are the two complex number operands
with an operator between them. On the right for each of the first four items
is the resulting complex number, shown by giving its real and imaginary
parts. For the last item, the result is the True/False value
given by a==c and b==d.
Here is the start of a Python class to implement complex numbers
and their arithmetic.
class Complex(object):
def __init__(self, real, imag=0):
self.real = float(real) # real part
self.imag = float(imag) # imaginary part
def __add__(self, other):
return Complex(self.real + other.real, self.imag + other.imag)
|
- Show how to create an instance named r of the Complex class with
real part 2 and imaginary part 3.
r = Complex(2,3)
- Give code for the additional method: __str__, where
this should make available the complex number in part a) above in the form
2+3j or (2+3j), your choice. [It's ok if your
program writes: 2+−3j instead of 2−3j.]
def __str__(self):
return "(%.8g+%.8gj)" % (self.real, self.imag)
- Add instance methods getReal and getImag to
return the real and imaginary parts, respectively.
def getReal(self):
return self.real
def getImag(self):
return self.imag
- Give code for the additional methods: __sub__,
__mul__,__div__, and __eq__, where these use
the formulas above. (Python3 needs __truediv__.
Return None for a disallowed division.)
def __sub__(self,other):
return Complex(self.real - other.real,
self.imag - other.imag)
def __mul__(self,other):
return Complex(self.real * other.real -
self.imag * other.imag,
self.real * other.imag +
self.imag * other.real)
def __div__(self,other):
denom = other.real **2 + other.imag **2
if denom == 0:
return None
return Complex((self.real * other.real +
self.imag * other.imag)/denom,
(self.imag * other.real -
self.real * other.imag)/denom)
def __eq__(self,other):
return self.real == other.real and \
self.imag == other.imag
See the link:
Complex Numbers.
- Here is a test to see if the * and / operations are working
correctly. Let u have real part 1.0 and
imaginary part 0.0. Let v have real part 1.0 and
imaginary part 1.0. Then if we start with u
and multiply by v eight times (that is, keep multiplying by v),
the result should be 16.0+0.0j. Similarly, if we start with u
and divide by v eight times, the result should be 0.0625+0.0j.
For this part, write Python code using the Complex class above
to carry out these two calculations. Your code should use the
== operator to check the answers.
def test_loop1(): # 8 mults
r = Complex(1.0,1.0)
r16 = Complex(16.0, 0.0)
p = Complex(1.0, 0.0)
print p
for i in range(0,8):
p = p*r
sys.stdout.write(str(p) + " " +
str(p == r16) + '\n')
def test_loop2(): # 8 divisions
r = Complex(1.0,1.0)
r16th = Complex(0.0625, 0.0)
p = Complex(1.0, 0.0)
print p
for i in range(0,8):
p = p/r
sys.stdout.write(str(p) + " " +
str(p == r16th) + '\n')
sys.stdout.write("\nTest 8 mults\n")
test_loop1()
sys.stdout.write("\nTest 8 divisions\n")
test_loop2()
(Output)
Test 8 mults
(1+0j)
(1+1j) False
(0+2j) False
(-2+2j) False
(-4+0j) False
(-4+-4j) False
(0+-8j) False
(8+-8j) False
(16+0j) True
Test 8 divisions
(1+0j)
(0.5+-0.5j) False
(0+-0.5j) False
(-0.25+-0.25j) False
(-0.25+0j) False
(-0.125+0.125j) False
(0+0.125j) False
(0.0625+0.0625j) False
(0.0625+0j) True
Everything asked for above and more
is on the handout you got as you left the final:
Complex Numbers. When I decided to put
complex numbers on the final (chosen partly because they are so close
to the fractions that you implemented), I wanted a way to test the
implementation. I used the two loops I asked you to write, but
then decided to calculate (exp(0+1j) which should be -1,
using the infinite series for exp(x), which converges for all
x, even complex values.]
- (20) Python classes, inheritance:
I looked at a number of possibilities for a
question about inheritance, but they all seemed too hard. So
I fell back to a simple addition to our standard example:
The Circle class is just what we had before. Only
the Square class is new, and you were given that.
import sys
class Shape(object):
def __init__(self, x = 0, y = 0):
self.x = x # x-coord of center
self.y = y # y-coord of center
def __str__(self):
return self.whoami() + \
': x = ' + str(self.x) + \
', y = ' + str(self.y)
def area(self):
return 0
def whoami(self): # get name of class
return type(self).__name__
class Rectangle(Shape):
def __init__(self, length, width, x, y):
super(Rectangle, self).__init__(x, y)
self.length = length
self.width = width
def __str__(self):
return super(Rectangle, self).__str__() +\
", length = " + str(self.length) + \
", width = " + str(self.width) + \
", area = " + str(self.area())
def area(self):
return self.length * self.width
class Square(Rectangle):
def __init__(self, side, x, y):
super(Square,self).__init__(side,side,x,y)
def __str__(self):
return super(Square, self).__str__()
# Circle class here
class Circle(Shape):
pi = 3.14159
def __init__(self, r, x, y):
super(Circle, self).__init__(x, y)
self.radius = r
def __str__(self):
return super(Circle, self).__str__() + \
", radius = " + str(self.radius) + \
", area = " + str(self.area())
def area(self):
return self.radius ** 2 * self.pi
shape1 = Shape(3,4)
rect1 = Rectangle(4,6,2,7)
square1 = Square(5,1,3)
circle1 = Circle(3,2,5)
shapes = [shape1, rect1, square1, circle1]
for shape in shapes:
sys.stdout.write(str(shape.area()) + " ")
sys.stdout.write(str("\n"))
(Program output:)
0 24 25 28.27431
|
|
- Write a class named Circle, modeled after the
Rectangle class at the right. Circle should inherit
from Shape, it should have one instance variable radius, one
class variable pi=3.14159, and three methods:
__init__, __str__, and area. Of course the area
is pi*radius*radius.
See red section at left.
- Consider the Square class. Give the names of instance
variables that it inherits from its two superclasses.
Square inherits length and
width directly
from Rectangle, and it inherits x and y indirectly
from Rectangle,
since it inherits them from Shape.
- The statement square1=Square(5,1,3) creates an instance
of Square, using the parameters 5, 1, and 3.
Trace the initialization of the variables in Square
that occur in the two uses of super (first in Square
and then in Rectangle).
- The code at the left bottom produces the output shown at the end
of the listing at the left.
It might be surprising that this code even works at all
and doesn't produce one or more error messages.
What is surprising here? (Or weird, unexpected? Hint: suppose
you decided to print the four different areas with your own code.)
- The feature illustrated in part d) above is something we didn't talk
about in class, but it's an important part of Python,
and of Java and C++ as well. If you know the name of this
language feature, give it here. (Otherwise look it up later.)
|
c.
square1=Square(5,1,3) directly sets:
(Inside Rectangle:)
self.length = length (formal param) = side (actual param in Square) = 5
self.width = width (formal param) = side (actual param in Square) = = 5
self.x = super().x = 1
self.y = super().y = 3
(Inside Shape:)
self.x = 1
self.y = 3
Thus the square1 instance of Square has 4 variables:
length = 5
width = 5
x = 1
y = 3
(side is only a parameter in __init__ in Rectangle)
d. and e.
Parts d) and e) above are calling attention to the polymorphism
that is shown at the end of the example. This concept means that
a reference to an instance of a superclass can serve as a reference
to an instance of a subclass. Thus the variable shape contains
sequentially references to instances of 3 subclasses. The
area() method picks out the code for the correct instance.
If you later added another kind of shape, the actual loop could
stay the same and still work. (All this is the "surprise.")
Polymorphism is a big deal in O-O programming, supported by may
languages, including Java
and C++, where it is a non-trivial additional run-time overhead.
For example, in C++, Stroustrup (inventor of C++) wanted C programmers
to feel they were getting no performance hit at all when they switched
to C++. He admitted that there was a slight performance hit with
polymorphism, but of course that isn't even available in C.
]
|