|
CS 3721 Programming Languages Fall 2013 | |
Recitation 1. DFAs & NFAs
| ||
Week 1: Aug 28 - 30
| ||
Submit following directions at:
submissions
and rules at:
rules.
Deadlines are:
|
1. Contrasts: Read the page Contrasts. You must understand what the following contrasting terms mean and what the contrast is:
- Syntax versus Semantics .
- Run-time versus Compile-time .
- Translation versus Interpretation .
- Give one reason why a compiled program usually executes much faster than an interpreted program. (Just one reason and not too much for your answer.)
- Consider the following "C" program:
#include <whatever.h> int main() { int a[20]; double f, g; int x, y, z; scanf("%lf", &r); while ((a + f)%k != m) { h = f.g(); printf("%s\t%c\t", x, a); if(nonexistent(f,2)) M = 1; // blah, blah } }
2. Finite Automata: Read the page FAs. There are many terms, notations, and contrasts here. You must familiarize yourself with those you don't already know, especially the following:
- symbol (not defined), alphabet, sentence, language, Σ, Σ*, epsilon = ε.
- FA, state, transition, start state, terminal state
- NFA, DFA, how an NFA or DFA recognizes sentences from a language.
- Is this an NFA or a DFA? (Always give reasons!)
- Suppose the FA processes the string "13.2$"
(where '$' is just a terminator that we will often use.)
It will start in State 0 and proceed along from state to state
as it processes character after character:
1 3 . 2 $ 0 ---> 1 ---> 1 ---> 3 ---> 3 ---> 9 - Do the same for the string "13E+$"? Explain why the result means that it has not accepted the second string.
- Write several strings that are recognized by this FA, and give the sequence of states as above. Include enough examples of strings that are accepted so that every arrow of the diagram is used while accepting one of the example strings. (This does not include arrows pointing to "error" states.) Note: I intend for you to work out this problem "by hand". It is also permissible to write a program to simulate the given DFA, as in Problem 3 below, but there will be no additional credit for this.
Consider the finite automaton below. (State 9 is an "accepting" state and States 4 and 5 are "error" or "rejecting" states.)
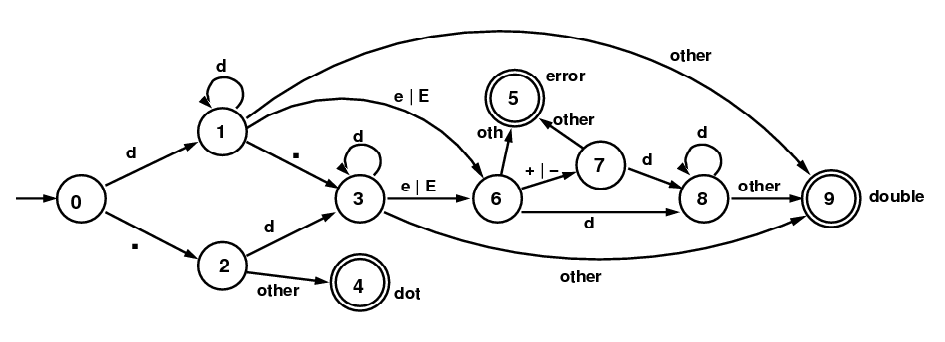
FSM for doubles, where "d" stands for any digit (the "suffix" is not included)
3. Simulating a DFA: Read the page FA Simulation. You must understand the following items:
- How a program can simulate the actions of a DFA.
- How a program can simulate the actions of an NFA. (We won't write any such programs.)
Write a program in C or in Java, perhaps similar to the one at abb (but it doesn't have to be similar), that will simulate (or model) the actions of the following DFA:
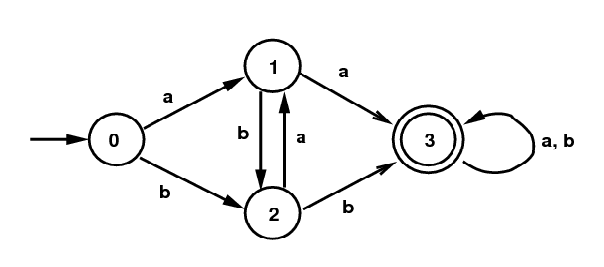
DFA for /(a|b)*(aa|bb)(a|b)*/
4. Subset Algorithm: Read the page Subset Algorithm. You must understand how this algorithm works and be able to carry it out "by hand" (not using a program).
- Use the subset algorithm to convert the following NFA
into a DFA that accepts the same language.
(Hint: The DFA also has 4 states.)
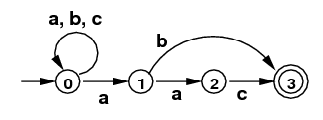
NFA for /(a|b|c)*(ab|aac)/
(Intuitively, any string of "a"s, "b"s, and "c"s,
ending in "ab" or "aac".) - Use the subset algorithm to convert the following NFA
into a DFA that accepts the same language.
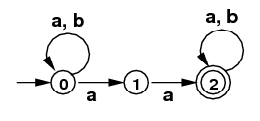
NFA for /(a|b)*(aa)(a|b)*/
(Intuitively, any string of "a"s, and "b"s,
containing "aa" somewhere.)
You must show your work. The answers should look like the items in the link above identified as "Tables".
Revision date: 2013-07-21. (Please use ISO 8601, the International Standard.)
