CS 3723  Programming Languages
Finite Automata

Notice that everything is finite except for the language, where in the interesting cases there are infinitely many sentences, as with the example above. We want to give finite descriptions of languages, including infinite languages. Consider another example: the set L of all strings of as and bs that end with "abb". The previous (English) sentence is an informal finite description. It would (of course) be impossible to list the elements of this language, but we could start: L = {abb, aabb, babb, aaabb, ababb, baabb, bbabb, aaaabb, aababb, ...}. The language L can be described or generated by the regular expression (a|b)*abb.

If Σ denotes the alphabet, then (using regular expression notation), Σ* denotes the set of all finite strings of symbols from the alphabet. This includes the empty string "", which is denoted by the lower-case Greek letter epsilon = ε. Thus any subset of Σ* is a language. (In particular, the sets Σ* of all finite strings, and the empty set Ø of no strings are languages.)

An FA consists of a finite set of states and finite set of transitions from state to state that occur as input symbols for the alphabet are processed. A transition can go from a state to itself. One state (never more than one) must be designated the start state or initial state. Any number of states (but at least one) must be designated the terminal states or final states or accepting states. Here is a diagram of an FA:

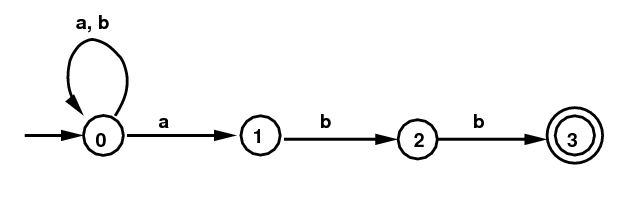
NFA for (a|b)*abb

Here the alphabet is {a, b} and the set of states is {0, 1, 2, 3}. The start state is 0, denoted by an initial arrow. There is only one terminal state, 3, denoted by a double circle around it.

• NFAs. The particular FA above is called a Non-Deterministic Finite Automaton (NFA).
  This NFA is said to recognize the language L above.

  In order to recognize strings from L with the NFA above, we process an input string character-at-a-time, starting with the 0th character. Start with the start state 0. For each character processed, follow a path labeled with that character. If we can manage (somehow) to end up in the terminal state 3 just as we finish all the characters in the string, we accept the string as belonging to L. Otherwise we reject the string.

  This automaton is called non-deterministic because there is a case (there must be at least one) with two possible choices for the arrow to take. Suppose we are processing the symbol a in the string "abaabaabb". How do we know when to leave state 0 and finish the string? (We could decide with a look-ahead buffer, but we want a simpler solution.)

• DFAs Given an NFA, it is always possible to create what is called a Deterministic Finite Automaton (DFA) that recognizes the same language. For the language L above, here is the corresponding DFA:
  
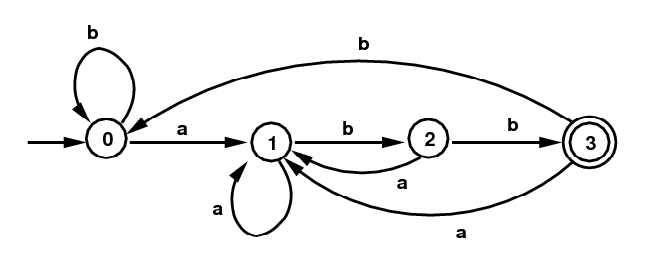
  DFA for (a|b)*abb

  This automaton is called deterministic because in each case there is exactly one choice for which arrow to follow. The process is uniquely determined. If you end up in the terminal state 3, and have reached the end of the string, then you accept the input string as belonging to L and otherwise you reject it.