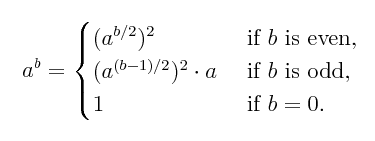CS 3723
 Programming Languages 
   Activation Records  
  Functions & Recursion  

[Note: All parts of this page use integer features of MIPS.]

Activation Records in General. If one properly uses a stack at runtime to support function calls, this approach implements recursion "for free", without any additional effort. At run time, each called function is supported by an activation record, which is storage on the stack dedicated to that particular call of that specific function.

The MIPS architecture gives minimal hardware support for recursive functions, so everything must be done "by hand".

The activation record needs to provide storage (at runtime) for at least the following items:

  • The return address (address from which the function was called). A function might be called from any number of places, including from within itself (recursive call) from any number of places.

  • The value returned by the function (which might be a pointer).

  • Locations to hold values of actual parameters fed to the function. (These can be expressions.) After the function is called, these locations function as the formal parameters. They behave like local variables.

  • Space for (non-static, automatic) local variables used by the function.

The work below uses a running example of a function of two parameters: a "raise-to-a-power" function. This has two parameters and doesn't require any local variables besides registers, so the activation record will hold 4 items, as shown in the illustration below. (The order of these items was an arbitrary choice.) This diagram shows the stack before the function is called. The "stack pointer", denoted by $sp, points to one location beyond the top of the stack, that is, it points to the first available location. Since we are working with doubles, we will only consider 8-byte items on the stack, although the return address takes up only 4 bytes.

[The diagrams show the special MIPS "stack pointer" $sp used to access the MIPS system stack. This is what one would normally use. In order to avoid any possible problems with the official stack pointer, I chose to allocate storage on a user-defined stack pointer, using the register $s2 for it. We have been using $s1 to save the return address of our MIPS function main.]

In the diagram below, the stack pointer "old $sp" might be pointing to the bottom of the stack, with nothing below it. Alternatively, which is below will be the mostly recently called function that is still active (has not yet returned). Assume that the next thing to do is to call a function (in fact a pow or rtp function). The old $sp calculates the two actual parameters, and inserts them into the stack, into locations that will be part of the activation record of the function to be called. These locations are shown in red below.

Stack for Activation Records: Before Function Is Called,
First Insert Parameter Values
                   STACK
                |              |                    |  Next (recursive)
                |--------------|                    |  Activation
                |              |                    |  Record
             ===|==============|===          -------+
   old -24 ---> |  Insert P2   |                    |
                |--------------|                    |  Space for Next
   old -16 ---> |  Insert P1   |                    |  Activation
                |--------------|                    |  Record
   old -8  ---> |              |                    |  (or first one)
                |--------------|                    |  
   old $sp ---> |              |                    |
             ===|==============|===          -------+
   old +8  ---> |  Parameter 2 |                    |
                |--------------|                    |  Previous (current)
   old +16 ---> |  Parameter 1 |                    |  Activation
                |--------------|                    |  Record
   old +24 ---> | Return value |                    |  (if present)
                |--------------|                    |  
   old +32 ---> | Return addr  |                    |
             ===|==============|===         --------+

After the function is called (control is passed to the function), the function first allocated an activation record on the stack, in this example by decrementing the $sp by 32 ($sp = $sp - 32). (This stack is growing toward smaller memory locations.) The function can now "find" the values of actual parameters at known offsets. These locations become the formal parameters for the function. First the function inserts its return address into the activation record (MIPS gives access to this return address). Then the function does its computations, ending with a value to return, which is inserted into the activation record. During its execution, the function may have called other functions, and each of those will push additional activation records onto the stack. By the time this function returns, all other called functions will have returned, so there is nothing above the current activation record. Finally, the called function deletes (deallocates) its activation record by incrementing $sp by 32. The function then returns control to the place from which is was called.

[It's important to realize that there is only one register $sp. "Old" and "new" above refer to different values stored in the register at different times.]

Stack for Activation Records: Function Executes,
Insert RetAdd, Calculate and Insert Return Value
                   STACK
                |              |                    |  Next (recursive)
                |--------------|                    |  Activation
                |              |  <--- new $sp      |  Record
             ===|==============|===          -------+
   old -24 ---> |  Parameter 2 |  <--- new +8       |
                |--------------|                    |  New (current)
   old -16 ---> |  Parameter 1 |  <--- new +16      |  Activation
                |--------------|                    |  Record
   old -8  ---> | Insert RetVal|  <--- new +24      |  
                |--------------|                    |  
   old $sp ---> | Insert RetAdd|  <--- new +32      |
             ===|==============|===          -------+
   old +8  ---> |  Parameter 2 |                    |
                |--------------|                    |  Old (previous)
   old +16 ---> |  Parameter 1 |                    |  Activation
                |--------------|                    |  Record
   old +24 ---> | Return value |                    |  (if present)
                |--------------|                    |  
   old +32 ---> | Return addr  |                    |
             ===|==============|===         --------+

Now, as shown below, the calling function can access the value returned by the function that it called. The calling function will usually have its own activation record (as shown), but it is the main function, it will have no activation record.

Stack for Activation Records: After Function Returns,
Retrieve Return Value
                   STACK
                |              |                    |  Next (recursive)
                |--------------|                    |  Activation
                |              |   <--- new $sp     |  Record
             ===|==============|===          -------+
   old -24 ---> |  Parameter 2 |   <--- new +8      |
                |--------------|                    |  Old deallocated
   old -16 ---> |  Parameter 1 |   <--- new +16     |  Activation
                |--------------|                    |  Record
   old -8  ---> |Retrieve RetV |   <--- new +24     |  
                |--------------|                    |  
   old $sp ---> |  Old RetAdd  |   <--- new +32     |
             ===|==============|===          -------+
   old +8  ---> |  Parameter 2 |                    |
                |--------------|                    |  Current (restored)
   old +16 ---> |  Parameter 1 |                    |  Activation
                |--------------|                    |  Record
   old +24 ---> | Return value |                    |  (if present)
                |--------------|                    |  
   old +32 ---> | Return addr  |                    |
             ===|==============|===         --------+

Our Specific Example: c = a ^ b. We will start with a simple pow function:

The table on the right below shows a Python function to do the calculation using a loop, and another function using recursion and based on the definition above.

Python a^b Functions Output
# atob.py: find c = a^b
import sys

def pow0(a, b): # loop
    c = 1
    while b != 0:
        c = c*a
        b = b - 1
    return c

def powr(a, b): # recursion
    if b == 0:
        return 1
    return a*powr(a, b-1)

def powd(a, b): # recursion debug
    if b == 0:
        res = 1
    else:
        res = a*powd(a, b-1)
    output("Call:   ", a, b, res)
    return res

def output(s, a, b, c):
    sys.stdout.write(s + "a:%.17g" % a)
    sys.stdout.write(", b:%.17g" % b)
    sys.stdout.write((", a^b:%.17g" % c)
      + "\n")

a = float(raw_input( "-->" ))
b = float(raw_input( "-->" ))
c = pow0(a, b)
cr = powr(a, b)
output("Loop:   ", a, b, c)
output("Recurs: ", a, b, cr)
# cd = powd(a, b) # only for 7^10, .9^7
# output("debug:  ", a, b, cd) # ditto

% python atob.py
-->7
-->10
Loop:   a:7, b:10, a^b:282475249
Recurs: a:7, b:10, a^b:282475249
Call:   a:7, b:0, a^b:1
Call:   a:7, b:1, a^b:7
Call:   a:7, b:2, a^b:49
Call:   a:7, b:3, a^b:343
Call:   a:7, b:4, a^b:2401
Call:   a:7, b:5, a^b:16807
Call:   a:7, b:6, a^b:117649
Call:   a:7, b:7, a^b:823543
Call:   a:7, b:8, a^b:5764801
Call:   a:7, b:9, a^b:40353607
Call:   a:7, b:10, a^b:282475249
debug:  a:7, b:10, a^b:282475249

-->1.6180339887498949
-->28
Loop:   a:1.6180339887498949, b:28, a^b:710646.99999859335
Recurs: a:1.6180339887498949, b:28, a^b:710646.99999859335

-->2
-->31
Loop:   a:2, b:31, a^b:2147483648
Recurs: a:2, b:31, a^b:2147483648

-->0.9
-->7
Loop:   a:0.90000000000000002, b:7, a^b:0.47829690000000014
Recurs: a:0.90000000000000002, b:7, a^b:0.47829690000000014
Call:   a:0.90000000000000002, b:0, a^b:1
Call:   a:0.90000000000000002, b:1, a^b:0.90000000000000002
Call:   a:0.90000000000000002, b:2, a^b:0.81000000000000005
Call:   a:0.90000000000000002, b:3, a^b:0.72900000000000009
Call:   a:0.90000000000000002, b:4, a^b:0.65610000000000013
Call:   a:0.90000000000000002, b:5, a^b:0.59049000000000018
Call:   a:0.90000000000000002, b:6, a^b:0.53144100000000016
Call:   a:0.90000000000000002, b:7, a^b:0.47829690000000014
debug:  a:0.90000000000000002, b:7, a^b:0.47829690000000014

Now I want to code these by hand into MIPS. I want to take input variables a and b, calculating a^b, and leaving the result in a variable c. However, in order to keep things simpler and shorter, I'm not using any memory locations below for variables, but I'm only using registers and the activation records. How the double registers are used is shown in the first table on the left below.

The MIPS program pow0.s on the left below shows a very simple loop to calculate a^b, using the register conventions. The MIPS program powr.s on the right uses recursion instead of a loop. This program uses a single sequence of recursive calls, so that at the end we can see all the activation records that were used. (None of the storage was overwritten during execution. In more complex programs, the stack of activation records might grow and shrink many times.) The diagram on the left below shows the 11 activation records used to calculate 7^10, at levels 0 (the first one), through 10.

Variables to Registers
# mapping of variables to registers:
#        $f0  (used for input)
#    a = $f2
#    b = $f4
#    c = $f6  (at end c=a^b)
#    0 = $f8  (constant)
#    1 = $f10 (constant)
#        $f12 (used for output)
#        $f14 (for return value)
#    2 = $f16 (constant)
#        $f18 (temporary)
#
#        $s1  (address of M)
#        $s2  (address of stack)
Level Activation Records for 7^10
P 2P 1 Return ValueRet Addr
10071 4194656
9177 4194656
82749 4194656
737343 4194656
6472401 4194656
55716807 4194656
467117649 4194656
377823543 4194656
2875764801 4194656
19740353607 4194656
0107282475249 4194396
 
a^b, with simple loop
### pow0.s: calculate c = a^b
main:   addu    $s7, $ra, $zero
# addr of M: constants, vars, temps
        la      $s1, M 
# read a as double
        li      $v0, 7
        syscall
        mov.d   $f2, $f0
# read b as double
        li      $v0, 7
        syscall
        mov.d   $f4, $f0
### end reading, start processing
        l.d     $f8, 0($s1)    # 0.0
        l.d     $f10, 8($s1)   # 1.0
        l.d     $f6, 8($s1)    # c=1
WhileStart0:
        c.eq.d  $f4, $f8       # if b==0
        bc1t    WhileEnd0      # goto 

        mul.d   $f6, $f6, $f2  # c=c*a
        sub.d   $f4, $f4, $f10 # b=b-1
        j       WhileStart0
WhileEnd0:
### return to system
        addu    $ra, $s7, $zero
        jr      $ra
        .data
        .align  3
M:      .double 0.,1.
Blank:  .asciiz " "
NewL:   .asciiz "\n"

<−− Red at left = return to main.

a^b, recursive
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
 
### powr.s: act. records and recursion
main:   addu    $s7, $ra, $zero
# addr of S, M: stack, constants
        la      $s2, S stack (act recs)
        la      $s1, M const 0.0, 1.0
### start of compiled code
# 2 constants
        l.d     $f8,   0($s1)  # 0.0
        l.d     $f10,  8($s1)  # 1.0
# read a as double, store as param1
#   in the activation record
        li      $v0, 7
        syscall
        s.d     $f0, -16($s2)
# read b as double, store as param2
#   in the activation record
        li      $v0, 7
        syscall
        s.d     $f0, -24($s2)
# call function
        jal     pow
        l.d     $f14, -8($s2)  # ret val
# print return value, obtained
#   from the activation record
        li      $v0, 3
        l.d     $f12, -8($s1)
        syscall
# print NewL as ASCII char
        li      $v0, 4
        la      $a0, NewL
        syscall
# return to system
        addu    $ra, $s7, $zero
        jr      $ra
########## body of pow function #######
pow:
# push activation record
        addi    $s2, $s2, -32
# save return address on stack
        sw      $ra, 32($s2)
# load parameters from activation record
        l.d     $f2, 16($s2)   # a
        l.d     $f4, 8($s2)    # b
# main part of function
        l.d     $f6, 8($s1)    # c=1
# check for end to recursion
        c.eq.d  $f4, $f8       # if b==0
        bc1t    RecursEnd
# get ready for recursive call
        sub.d   $f4, $f4, $f10 # b=b-1
# insert 1st and 2nd parameters
        s.d     $f2, -16($s2)  # a
        s.d     $f4, -24($s2)  # b-1
# call function (recursive)
        jal     pow
        l.d     $f14, -8($s2)  # ret val
# multiply value returned by a
        mul.d   $f6, $f14, $f2 # c=c*a
RecursEnd:
# insert return value
        s.d     $f6, 24($s2)
# restore return address from stack
        lw      $ra, 32($s2)
# pop activation record
        addi    $s2, $s2, 32
# return
        jr      $ra
######### end of pow function #########
        .data
        .align  3
T:      .space  1000
S:
M:      .double 0.,1.
Blank:  .asciiz " "
NewL:   .asciiz "\n"
Tab:    .asciiz "\t"

Overview of execution:
main: 8-21, call pow

pow:  repeat 10 times: 36-55
      call pow recursively
      each time push one AR

pow:  36-48, 61-67, push last AR
      return from pow to pow

pow;  repeat 10 times: 56-67
      multipy by a; delete one AR
      return from pow to pow

main: return to main to after call to pow.
      22-35, print ans, return to system
 
Trace of pow, inputs 7.0 and 10.0
 Lines Action Synbols
m
a
i
n
8-9 Load constants 0.0, 1.0 $f8=0.0; $f10=1.0
12-19 Read inputs: 7.0, 10.0
Store as params into AR0 		AR0[0]=10.0;
AR0[1]=7.0;
21 Call pow jal pow
A
R
0
36 Start executing pow pow:
38 Allocate AR0 (includes 2 params)
40 Save return address in AR0 AR0[3] = $ra
42-43 Load params from AR0 into regs
7.0 into $f2, 10.0 into $f4 		$f2=AR0[1];
$f4=AR0[0];
45 Load 1.0 into $f6, value to return $f6=1.0
47 Check $f4 (== 10.0) against 0.0 $f4!=0.0
48 do NOT branch to RecursEnd continue at line 50
50 Subtract 1 from $f4 $f4=$f4-1;
($f4==9.0)
52-53 Store params (7.0,9.0) into AR1 AR1[1]=$f2 (==7.0)
AR1[0]=$f4 (==9.0)
55 Call pow recursively jal pow
A
R
1
36 executing pow again pow:
38-55 Same as before, except:
AR0 ==> AR1; AR1 ==> AR2;
10.0 ==> 9.0; 9.0 ==> 8.0
Act Recs: AR2 through AR9, with 8.0 through 1.0
A
R
1
0
36 executing pow again pow:
38-47 Similar to before, except:
AR9 ==> AR10; 1.0 ==> 0.0;
48 DO branch to RecursEnd (line 59).
Do NOT call pow 		RecursEnd:
61 Insert return value into AR10[2] AR10[2]=$f6
63 Restore return address from AR[3] $ra=AR10[3]
65 Delete current activation record
67 Use $ra above to return. jr $ra
A
R
9
56 return to just after call to pow
56 return to just after call to pow
load return value from AR10[2] 		$f14 = AR10[2];
58 mult ret value by a, store in $f6 mul.d $f6,$f14,$f2
61 Insert ret value into act rec AR10[2]=$f6
63-67 Just as above
Act Recs: AR8 down to AR0, mul-->t by 7.0 each time.
Last return goes back to line 22 in main program.
m
a
i
n
22 Load ret value from AR0 into $f12
25-27 Print return value
29-31 Print newline
31-35 Return to system

Fancy Exponentiation. This example uses a more complex raise-to-a-power algorithm, given by the equations below. Here the recursion is essential, unless one completely rewrites the algorithm. However, again in this case there is only a single tower of recursive calls, so that a dump at the end again shows all the activation records. At the end are two tables showing them for example runs.

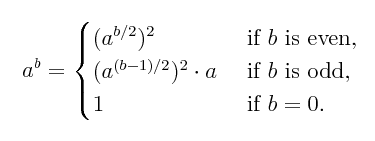
Python a^b Functions Output
# atob_fancy.py: find c = a^b
import sys

def atob(a, b): # formula
    if b == 0:
        return 1
    if b%2 == 0:
        return atob(a, b/2)**2
    return atob(a, (b-1)/2)**2 * a

def atobd(a, b): # debug version
    if b == 0:
        res = 1
    elif b%2 == 0:
        res = atobd(a, b/2)**2
    else:
        res = atobd(a, (b-1)/2)**2 * a
    output("Call:  ", a, b, res)
    return res

def output(s, a, b, c):
    sys.stdout.write(s +  "a:%.17g" % a)
    sys.stdout.write(   ", b:%.17g" % b)
    sys.stdout.write((", a^b:%.17g" % c)
      + "\n")

a = float(raw_input( "-->" ))
b = float(raw_input( "-->" ))
c = atob(a, b)
output("Fancy: ", a, b, c)
sys.stdout.write("\nDebug version:\n")
c = atobd(a, b)
output("Debug: ", a, b, c)

% python atob_fancy.py
-->1.6180339887498949
-->57
Fancy: a:1.6180339887498949, b:57, a^b:817138163596.00073
Debug version:
Call:  a:1.6180339887498949, b:0, a^b:1
Call:  a:1.6180339887498949, b:1, a^b:1.6180339887498949
Call:  a:1.6180339887498949, b:3, a^b:4.2360679774997898
Call:  a:1.6180339887498949, b:7, a^b:29.034441853748636
Call:  a:1.6180339887498949, b:14, a^b:842.99881375871053
Call:  a:1.6180339887498949, b:28, a^b:710646.99999859312
Call:  a:1.6180339887498949, b:57, a^b:817138163596.00073
Debug: a:1.6180339887498949, b:57, a^b:817138163596.00073

-->2
-->973
Fancy: a:2, b:973, a^b:7.9833612381388792e+292
Debug version:
Call:  a:2, b:0, a^b:1
Call:  a:2, b:1, a^b:2
Call:  a:2, b:3, a^b:8
Call:  a:2, b:7, a^b:128
Call:  a:2, b:15, a^b:32768
Call:  a:2, b:30, a^b:1073741824
Call:  a:2, b:60, a^b:1.152921504606847e+18
Call:  a:2, b:121, a^b:2.6584559915698317e+36
Call:  a:2, b:243, a^b:1.4134776518227075e+73
Call:  a:2, b:486, a^b:1.997919072202235e+146
Call:  a:2, b:973, a^b:7.9833612381388792e+292
Debug: a:2, b:973, a^b:7.9833612381388792e+292

Below is the recursive version of this program translated to MIPS using activation records as in the previous program.

a^b, Fancy Algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
 
### rtp.s: use activation records
main:   addu    $s7, $ra, $zero
# addr of S, M: stack, constants
        la      $s2, S stack (act recs)
        la      $s1, M const (0,1,2)
# 3 constants
        l.d     $f8,   0($s1) # 0.0
        l.d     $f10,  8($s1) # 1.0
        l.d     $f16, 16($s1) # 2.0
# read a as double, store as param1
        li      $v0, 7
        syscall
        s.d     $f0, -16($s2)
# read b as double, store as param2
        li      $v0, 7
        syscall
        s.d     $f0, -24($s2)
# call function
        jal     rtp
# get return value
        l.d     $f14, -8($s2)
# print return value
        li      $v0, 3
        l.d     $f12, -8($s1)
        syscall
# print NewL as ASCII char
        li      $v0, 4
        la      $a0, NewL
        syscall
# return to system
        addu    $ra, $s7, $zero
        jr      $ra
######### body of rtp function ####
rtp:
# push activation record
        addi    $s2, $s2, -32
# save return address on stack
        sw      $ra, 32($s2)
# load parameters
        l.d     $f2, 16($s2) # a
        l.d     $f4, 8($s2)  # b
# start main part of function
        l.d     $f6, 8($s1)  # c=1
# check for end to recursion
        c.eq.d  $f4, $f8 # if b==0
        bc1t    RecursEnd

# next check for even b
        div.d   $f18, $f4, $f16  # t1 = b/2
        trunc.w.d $f18, $f18  # trunc(b)
        cvt.d.w $f18, $f18    # to double
        mul.d   $f18, $f18, $f16 # mult by 2
        sub.d   $f18, $f4, $f18
        c.eq.d  $f18, $f8  # res comp to 0
        bc1f    BisOdd
# here b is non-zero and even
  # get ready for recursive call
        div.d   $f4, $f4, $f16 # b = b / 2
  # insert 1st and 2nd parameters
        s.d     $f2, -16($s2)  # a
        s.d     $f4, -24($s2)  # b/2
  # call function (recursive)
        jal     rtp
        l.d     $f14, -8($s2) # return val
  # square return value, result in c
        mul.d   $f6, $f14, $f14  # c = ret^2
        b       RecursEnd
BisOdd:
# here b is non-zero and odd
  # get ready for recursive call
        sub.d   $f4, $f4, $f10 # b = b - 1
        div.d   $f4, $f4, $f16 # b = b / 2
  # insert 1st and 2nd parameters
        s.d     $f2, -16($s2)  # a
        s.d     $f4, -24($s2)  # (b-1)/2
  # call function (recursive)
        jal     rtp
        l.d     $f14, -8($s2) # return val
  # square return value, result in c
        mul.d   $f6, $f14, $f14  # c = ret^2
  # multiply by a
        mul.d   $f6, $f6, $f2
RecursEnd:
# insert return value
        s.d     $f6, 24($s2)
# restore return address from stack
        lw      $ra, 32($s2)
# pop activation record
        addi    $s2, $s2, 32
# return
        jr      $ra
######### end of rtp function ###########
        .data
        .align  3
T:      .space  1000
S:
M:      .double 0.,1.,2.
Blank:  .asciiz " "
NewL:   .asciiz "\n"

Level Activation Records for 2^973
P 2P 1 Return ValueRet Addr
100 21 4194720
9 1 22 4194720
8 3 28 4194720
7 7 2128 4194720
6 15 232768 4194688
5 30 21073741824 4194688
4 60 21.15292150e+18 4194720
3 12122.65845599e+36 4194720
2 24321.41347765e+73 4194688
1 48621.99791907e+1464194720
0 97327.98336123e+2924194400
Red = return to main.

LActivation Records for φ^57 (Return Value)/sqrt(5)
P
2		P
1		 Return ValueReturn
Address
60φ1 4194720 0.4472135954999579≐F(0)=0
51φ1.61803398874989494194720 0.7236067977499789≐F(1)=1
43φ4.236067977499789814194720 1.8944271909999157≐F(3)=2
37φ29.03444185374863554194688 12.984597134749391≐F(7)=13
214φ842.9988137587105264194688 377.0005305032323≐F(14)=377
128φ710646.9999985931214194720 317811.0000006294≐F(28)=317811
057φ817138163596.0007324194400 365435296162.0003≐F(57)=365435296162

Here is a python program (using high precision floats) that gives more accurate values for the last two floats above (see mpmath):

φ^28 and φ^57
% python power.py
from mpmath import *
import sys

mp.dps = 80
print "Precision: ", mp.dps

mp.dps = 100
print "Precision: ", mp.dps
five = mpf(5)
phi = (1 + sqrt(five))/2
print "phi: ", phi
print "phi**200: ", phi**200
print "F(200): ", phi**200 / sqrt(five)

python power.py
Precision:  80
phi:    1.618033988749894848204586834365638117720309179805
phi^28: 710646.9999985928316027479464165778158308091807432
phi^57: 817138163596.0000000000012237832530049452374054045
F(57) : 365435296161.9999999999994527074913110237343018279
                 1         2         3         4         5
        12345678901234567890123456789012345678901234567890

φ^28 and φ^57
from mpmath import *
import sys

mp.dps = 100
print "Precision: ", mp.dps
five = mpf(5)
phi = (1 + sqrt(five))/2
print "phi: ", phi
print "phi**200: ", phi**200
print "F(200): ", phi**200 / sqrt(five)

% python power.py
Precision:  100
phi:
1.618033988749894848204586834365638117720309179805762862135448622705260462818902449707207204189391137
phi**200:
627376215338105766356982006981782561278126.9999999999999999999999999999999999999999984060600712108932
F(200):
280571172992510140037611932413038677189525.0000000000000000000000000000000000000000007128316065647239
                                                                                                   1 
         1         2         3         4         5         6         7         8         9         0 
12345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901

(Revision date: 2014-11-09. Please use ISO 8601, the International Standard.)