CS 3343
 Analysis of Algorithms 
  Undecidable Problems   

Introduction. Before reading this page, you should first read Turing Machines. Here we present a short list of undecidable problems, that is, problems which no computer program can solve.

Students may have heard of unsolvable problems such as "trisecting an angle" (constructing an angle a third the size of a given angle) or "squaring the circle" (constructing a square with the same area as a given circle), the latter phrase often used now by people who at best have a vague idea of its meaning. These problems are only unsolvable if you restrict to a ruler and compass for constructions, but the problems are easily solvable with better instruments.

The Halting Problem. This is the basic problem for computing machines. Wouldn't if be nice if we had a program which would input some other program (along with its input data) and would answer the question: Will the given input program running with the given input data eventually halt or will it run indefinitely, without ever halting? We could detect undesirable infinite loops and avoid other problems. Turing showed that no such algorithm or program can exist. Humanity will never be able to solve this problem. Of course specific instances of the problem can be solved, as when you detect an infinite loop, or when you run the program to completion. The general problem can never be solved.

Repeating: there cannot exist a single program that for all input finite programs (along with their finite data) will correctly answer the question: will the input program eventually halt or not when it is executed?

The proof is simple but annoyingly technical and confusing. It involves supposing such a program exists, and running it with itself as input data. Plus a further construction.

The Word Problem. I start with an example from my main reference:

Example of the Undecidable Word Problem:
Given an alphabet of three symbols a, b, c, and given three equations

    ba = abc
    bc = cba
    ac = ca
we can obtain other equations by substitution:
        bac = abcc
        bac = bca = cbaa = cabca = acbca = ...
= cabca = cabac = ...
= cabca = cacbaa = ...
(bold letters above are what is about to be replaced)
One might ask questioning like: "Can we deduce for the three equations that bacabca = acbca?"

The word problem for any finite set of equations is the general question: given an equation, can it be deduced from the given equations or not?

The word problem is undecidable, and the proof is not too difficult. It is necessary to model an arbitrary Turing machine T as an instance of the word problem. This is done is such a way that if one could solve this word problem, then one could solve the halting problem for T. Thus we are reducing the halting problem to the word problem.

In my own research I used a special case of the word problem (the word problem for a special type of group) to create a public-key cryptosystem: PKC.

Formal Computer Security. In the 1960 and 1970's came the need for access control management. Researchers introduced the notion of subject, object, and access control matrix. The latter keeps track of which subject has which type of access to which objects. Harrison, Ruzzo and Ullman showed in 1976 that security is inherently undecidable in a conventional access control matrix. The underlying reason for their conclusion is the fact that users can give away access rights on their own initiative and without constraints. (The following write-up is a shortened version of the Wikipedia article.)

The HRU security model defines a protection system consisting of a set of generic rights R and a set of commands C. An instantaneous description of the system is called a configuration and is defined as a tuple (S,O,P) of current subjects S, current objects O and an access matrix P.

Since the subjects are required to be part of the objects, the access matrix contains one row for each subject and one column for each subject and object. An entry for subject s and object o is a subset of the generic rights R.

The commands are composed of primitive operations and can additionally have a list of pre-conditions that require certain rights to be present for a pair (s,o) of subjects and objects. The primitive requests can modify the access matrix by adding or removing access rights for a pair of subjects and objects and by adding or removing subjects or objects.

Harrison, Ruzzo and Ullman showed that various questions about this HRU system are undecidable. They did this by simulating a Turing machine within the system.

The Game of Life. You are used to single-player games, two-player games, multi-player games, and so forth. Life is a zero-player game. The evolution of life is completely determined by its initial state.

Life is played on an infinite two-dimensional chessboard. All but finitely many cells are dead initially -- the others are live. Every cell interacts with its eight neighbors, which are the cells that are horizontally, vertically, or diagonally adjacent. Life proceeds from generation to generation following a very simple set of rules:

  1. Any live cell with fewer than two live neighbors dies by exposure.
  2. Any live cell with two or three live neighbors lives on to the next generation by survival.
  3. Any live cell with more than three live neighbors dies by overcrowding.
  4. Any dead cell with exactly three live neighbors becomes a live cell by reproduction.

Summary

Just 3 for BIRTH
2 or 3 for SURVIVAL
Otherwise DEATH

Here are some pictures from the Wikipedia article:

GliderSpace ship
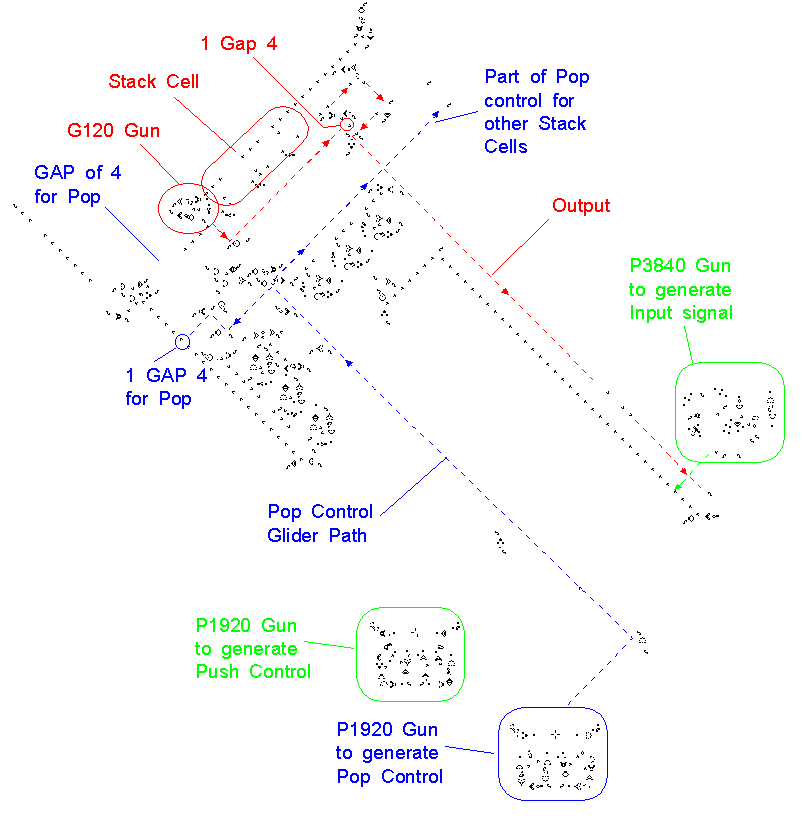
Glider GunPulsar
Glider Gun on a Torus (Donut)

On the page above are references to many constructions of Turing machines and of more capable computers using Life. Thus determining the outcome of Life evolution is undecidable. For example, Rendell's TM give details of the enormously complex task of implementing an arbitrary TM in Life. Below is an annotated picture of one component:

Revision date: 2012-04-23. (Please use ISO 8601, the International Standard Date and Time Notation.)