CS3343
 Analysis of Algorithms 
  Turing Machines   

Alan Turing: 2012 is officially the Year of Alan Turing, who was born on June 23, 1912. There is a lot of stuff on the web about him:
Centenary Celebration of Turing, Turing biography, Turing homepage (so to speak).

Overview: In the early 1930s, before there were any computing machines, Alan Turing addressed the issue of computation -- the power and subtle limitations of computations. He created what is now called a model of computation. Objects similar to his particular version have become known as Turing machines (TM). At this time there wasn't hardware to carry out computations, but his machines were a mathematical abstraction. Over the years others have created alternative models of computation, some radically different from Turing's model. All known models will carry out the same collection of computations. The Church-Turing Thesis is that there is no more powerful model.

You are surrounded by models of computation: each hardware computer is one such, as are each of the languages used to program these machines. None of these models is as powerful as a TM in one significant aspect: they all have limits to the size of their storage. A TM has unlimited storage. (Don't say infinite storage -- that probably has no meaning. A TM has an arbitrary amount of memory, and if more memory is needed, one can always add some.)

Turing wanted his model of computation to be as simple as possible. The model presented here is closer to a model by Emil Post, but these details are not important.

The Turing Machine: The storage of a TM is a linear tape of squares, each of which can contain either a '0' or a '1'. This tape extends arbitrarily far in each direction. Initially all squares are set to '0'. The tape interacts with a tape head, which is initially positioned at a square distinguished in no other way. The tape head can read what is no the square (one says "scan the square") to see if it is a '1' or a '0'. The tape head also interacts with a Turing program (TP), which consists of numbered sequence of instructions to be carried out. Instruction numbering begins with '1'. There are seven kinds of instructions: to print a '0' or a '1' onto the square being scanned, to move the tape head one square to the left of to the right, to stop (that is, halt execution), and to goto a numbered instruction in case a '0' or a '1' is scanned. Except for the conditional goto instructions, after executing an instruction, execution proceeds to the next instruction. Execution continues until a "stop" instruction is reached. It is possible for execution to continue indefinitely without reaching a "stop" instruction.

The Universal Turing Machine: Turing also conceived the idea of a single TM that could simulate the actions of any other TM (including itself!) by representing the other machine in coded form on the Turing tape itself, as shown below. Then the Universal TM (which was described in complete detail) would simulate the actions of the machine on the tape. Thus Turing developed the idea of a stored program computer before there were any actual computers.

Doubling Program: The table on the left below gives the seven available instructions. The table on the right gives an example program. Along with the program, one must know the initial tape contents, and the initial square being scanned. (All non-zero tape squares are shown below, and the initial location of the tape head is shown by the line below the squares.)

The tape is only accessible through the tape head, so only the single square being scanned in accessible, until "move left" or "move right" instructions move the head to another square. (There is no random access to the tape; tape squares have nothing like an address attached to them.)

Instructions in the Turing Language
InstructionRepresentation Op
Code
print 0 000 0
print 1 001 1
move left 010 2
move right 011 3
stop 100 4
if 0 is scanned
 goto i		 101 0...0 1
    <-i->		 5
if 1 is scanned
 goto j		 110 1...1 0
    <-j->		 6
(end marker) 111 -
 
Doubling Program
InstructionRepresentation
 1. print 0
 2. move left
 3. if 1 is scanned goto 2
 4. print 1
 5. move right
 6. if 1 is scanned goto 5
 7. print 1
 8. move right
 9. if 1 is scanned goto 1
10. stop
    (end)

Initial   ...0000110000...
 tape:           |

000
010
110 11 0
001
011
110 11111 0
001
011
110 1 0
100
111

The flowchart below describes how the doubling program works. In this material, the term "blank" or "blank square" just means a zero or a square with a zero in it.

The table below gives a trace of the execution of the program on the above right. Just before each instruction is executed, this gives the portion of the tape with 1's on it, along with a vertical line below the tape showing where the tape head is positioned. In addition, the "lc" or "location counter" is given: the location in the TP of the next instruction to be executed. Also the "op code" from the third column of the table above on the left: the integer code for the instruction. Finally, "ec", the "execution counter" counts the instructions as they are executed. The value of the variable "scan" gives the integer locations of the tape head from the simulator. (This value is an artifact of the particular storage used by the simulator for the tape.)

Trace of execution of the doubling program
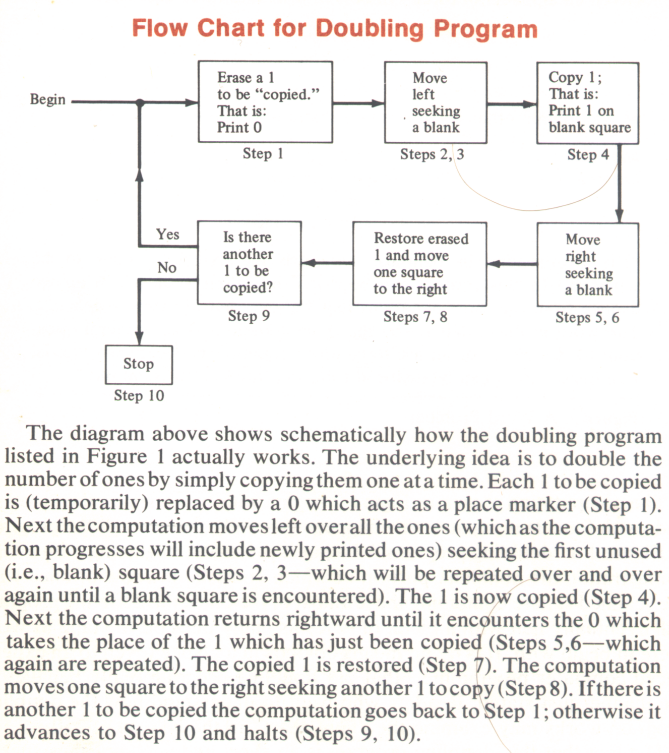
lc = location counter; op = op code;
scan = square scanned; ec = execution counter;
line points to square being scanned;

00000000001100000000 lc:1,op:0,scan:100,ec:1
          |
00000000000100000000 lc:2,op:2,scan:100,ec:2
          |
00000000000100000000 lc:3,op:6,scan:99,ec:3
         |
00000000000100000000 lc:4,op:1,scan:99,ec:4
         |
00000000010100000000 lc:5,op:3,scan:99,ec:5
         |
00000000010100000000 lc:6,op:6,scan:100,ec:6
          |
00000000010100000000 lc:7,op:1,scan:100,ec:7
          |
00000000011100000000 lc:8,op:3,scan:100,ec:8
          |
00000000011100000000 lc:9,op:6,scan:101,ec:9
           |
00000000011100000000 lc:1,op:0,scan:101,ec:10
           |
00000000011000000000 lc:2,op:2,scan:101,ec:11
           |
00000000011000000000 lc:3,op:6,scan:100,ec:12
          |

00000000011000000000 lc:2,op:2,scan:100,ec:13
          |
00000000011000000000 lc:3,op:6,scan:99,ec:14
         |
00000000011000000000 lc:2,op:2,scan:99,ec:15
         |
00000000011000000000 lc:3,op:6,scan:98,ec:16
        |
00000000011000000000 lc:4,op:1,scan:98,ec:17
        |
00000000111000000000 lc:5,op:3,scan:98,ec:18
        |
00000000111000000000 lc:6,op:6,scan:99,ec:19
         |
00000000111000000000 lc:5,op:3,scan:99,ec:20
         |
00000000111000000000 lc:6,op:6,scan:100,ec:21
          |
00000000111000000000 lc:5,op:3,scan:100,ec:22
          |
00000000111000000000 lc:6,op:6,scan:101,ec:23
           |
00000000111000000000 lc:7,op:1,scan:101,ec:24
           |
00000000111100000000 lc:8,op:3,scan:101,ec:25
           |
00000000111100000000 lc:9,op:6,scan:102,ec:26
            |

The above gives a run doubling 2 1's to 4 here, (27 instructions executed).
A run doubling 3 1's to 6 is here, (52 instructions executed).
A run doubling 4 1's to 8 is here, (85 instructions executed).

Here is another way to visualize the actions of this doubling program. I have grouped instructions 1-3 together and call them A. Similarly I call 4-6 B, 7-8 C, and 9-10 D. Now I trace through the doubling program using the groups A, B, C, and D, first with 2 ones and then with 3 ones.

2n+1 Program: The next program converts n 1s on the tape into 2n+1 1s on the tape. It uses the previous program as a sort of subroutine, so that for each 1 it finds, it doubles the result.

Exponentiation Program
InstructionRepresentation
 1. print 0
 2. move left
 3. if 1 is scanned goto 2
 4. print 1
 5. move right
 6. if 1 is scanned goto 5
 7. print 1
 8. move right
 9. if 1 is scanned goto 1
10. move right
11. if 0 is scanned goto 22
12. move right
13. if 1 is scanned goto 12
14. move left
15. print 0
16. move left
17. if 1 is scanned goto 16
18. move left
19. if 1 is scanned goto 18
20. move right
21. if 1 is scanned goto 1
22. stop
23. end

Initial  ...0000010110000...
 tape:           |

000
010
110 11 0
001
011
110 11111 0
001
011
110 1 0
011
101 0000000000000000000000 1
011
110 111111111111 0
010
000
010
110 1111111111111111 0
010
110 111111111111111111 0
011
110 1 0
100
111

A run producing 8 1's is here (162 instructions executed).
A run producing 16 1's is here (494 instructions executed).

The TM: The instruction traces above were produced by a simple TM simulator in Java: simulator.
Note: This material is adapted from an elegant essay by Martin Davis: What is a Computation?, 1978.

Revision date: 2011-11-24. (Please use ISO 8601, the International Standard Date and Time Notation.)