Be sure to establish the base case (n = 1), as well as proving that if the result holds for an arbitrary n, then it holds for n+1.

[I've "borrowed" Mr. Munsterteiger's nice-looking Ascii solution. (Note: You are NOT being graded on the attractiveness of your solutions, but on their accuracy.)

                     _     _       _              _
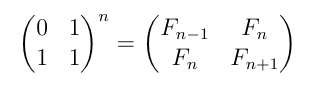
                    | 0   1 |^n   | F(n-1)   F(n)  |
Need to prove that  |_1   1_|   = |_F(n)    F(n+1)_|, for all n >= 1

Let n = 1
-----------
 _     _       _     _
| 0   1 |^1   | 0   1 |
|_1   1_|   = |_1   1_|

This is true because:
F(n-1) = F(1-1) = F(0) = 0
F(n)   = F(1)   = 1
F(n+1) = F(1+1) = F(2) = 1
                 _     _        _              _
                | 0   1 |^k    | F(k-1)   F(k)  |
Now assume that |_1   1_|    = |_F(k)    F(k+1)_|, for any k >= 1
                                 
Now let n = k + 1

To prove:
 _     _            _                 _
| 0   1 |^(k+1)    | F(k)      F(k+1) |
|_1   1_|        = |_F(k+1)    F(k+2)_|
------------------
 _     _            _     _    _     _
| 0   1 |^(k+1)    | 0   1 |^k| 0   1 |
|_1   1_|       =  |_1   1_|  |_1   1_|
                    _              _  _     _
                   | F(k-1)   F(k)  || 0   1 |  (Based on assumption
                =  |_F(k)    F(k+1)_||_1   1_|         from above)
                    _                                      _
                   | F(k-1)*0 + F(k)*1    F(k-1)*1 + F(k)*1 | (Multiplying)
                =  |_F(k)*0 + F(k+1)*1    F(k)*1 + F(k+1)*1_|     
                    _                      _
                   | F(k)     F(k-1) + F(k) | (Simplifying)
                =  |_F(k+1)   F(k) + F(k+1)_|
                    _             _
                   | F(k)   F(k+1) | (Using the definition of Fibonacci Sequence)
                =  |_F(k+1) F(k+2)_|

We have proved that
  o the identity holds for n=1,
  o if it holds for an arbitrary k >= 1, then it holds for k + 1

So by induction, we conclude that the Fibonacci matrix identity is true.]

Say briefly what the Leonardo Numbers are and where we encountered them.
Use induction to prove the following formula:

[The nth Leonardo number A_n has many uses but we encountered it when studying the recursive definition of F_n. A_n is the number of nodes in the recursion tree of function calls in calculating F_n recursively. We mentioned them in class and in the notes for the Weird Topic: 5 Fibonacci Matrix 1.

You have to prove the formula holds for both base cases: A₀ = 1, and A₁ = 1. This is easy:

A₀ = 2 * F₀₊₁ - 1 = 2 * F₁ - 1 = 2 * 1 - 1 = 1

A₁ = 2 * F₁₊₁ - 1 = 2 * F₂ - 1 = 2 * 1 - 1 = 1

So we know the formula is true for all n >= 0.]

Note: The following kind of proof is NOT what you are to do:
"Based on the variable y, this program will clearly iterate y times. Each time, starting with 0, we keep adding x to a running sum. In the end, we've added in x a total of y times, so x + x + ... + x (y times) is obviously x*y, which is what mult is supposed to do."

// mult: inputs X and Y both > 0
int mult(int X, int Y) {
   int x = X, y = Y, p = 0;
   while (y > 0) {
      p = p + x;
      y = y - 1;
   }
   return p;
}

Use the "loop invariant" method to prove this program is correct by going through the following steps. (You might get help from the answers to Recitation 1, specifically Problem 4.)

1. Figure out or guess what the loop invariant must be. (I'll give this to you on Tuesday, 14 February 2012, right after the full-credit deadline.) [The only loop invariant that seems to make sense is:
   p + x * y = X * Y

2. Carefully write out a proof following the four steps given below:
   1. Prove that loop invariant is true initially. [Plugging in initial values, p + x * y = 0 + X * Y = X * Y.]
   2. Prove that after each execution of one iteration of the loop, the loop invariant is still true. [Use p', x', and y' for the new values of p, x, and y at the end of the loop. Then p' + x' * y' = (p + x) + x * (y - 1) = p + x + (x * y) - x = p + x * y.]
   3. Prove that on termination, the equation for the loop invariant shows that the correct value is being calculated. [I would be happier if I'd written the loop as "while (y != 0)", because then we could assert more easily that on termination one must have y == 0. In any event, if y is zero then the loop invariant says: p + x*0 = X*Y, or p = X*Y, and p is what we are returning.]
   4. Prove that the algorithm terminates. [The comment at the top of the function definition asserts that X and Y are both > 0. The function works correctly even if they are both >= 0. If Y == 0, then y == 0, and the function returns 0 as it should, If Y > 0, then y > 0. repeated subtraction of 1 from y must eventually bring it down to 0. Hence the loop must terminate.]

3. What goes wrong in the proof if one writes p = 1; in error instead of p = 0;? (Not just "how is your answer wrong?", but in addition, how does your proof given in (ii) above fail to work?) [Part (a) above fails: the loop invariant is not true initially. All the other parts work. So Part (b) is true, that is, if the loop invariant is true at the start of the loop, then it will be true at the end. But it is NOT true at the start of the loop. Similarly (c) and (d) work.]
4. What goes wrong in the proof if one writes y = y + 1; in error instead of y = y - 1;? [I meant to write a more interesting question: suppose I had written the loop as "while (y != 0)". Then I might ask: "What goes wrong with the proof if one writes y = y + 1 AND p = p - x (TWO ERRORS)?" In this more interesting case all parts work except (d). The loop invariant is true initially. Surprisingly, if it is true at the start, it will still be true at the end of any loop iteration. And IF the loop terminates, it will return the correct value. The only problem is that it won't terminate.]

1. What is the largest that the depth of a binary search tree with n nodes can be? Give an example of such a tree. (Describe such a tree or give a specific example.) [The largest the depth can get occurs when each node has only one non-null child, so the depth will be (n - 1), starting from 0 at the root.]

2. What is the smallest that the depth of a binary search tree with n nodes can be? Give an example of such a tree. (Describe such a tree or give a specific example.) [This would be the fully complete binary tree used for a heap. For a given depth k, the most nodes that such a tree can have is 2^(k+1) - 1. For a given value of n, the depth of a complete tree with n nodes is floor(log₂n).]

You can use binary search tree of chars (in both Java and C) as a pattern in constructing the tree for this section, or else you can use another binary search tree program that you wrote yourself, but not one from elsewhere.

1. Convert the tree at the above link to a binary search tree of doubles. (Alternatively, you may be working in Java with your own generic program that is already good for doubles.)

2. Arrange to insert random doubles into a growing tree, thus creating the desired randomly built binary search tree. (Various programs in the course show random doubles being generated.)

3. Add an extra field int depth to the struct or class representing a node in the tree.

4. Insert an integer value into each depth field that represents the distance down from the root node to the given node. (The root node should have depth 0. One way to do this is to use an inorder traversal with an extra parameter in the function whose value is the depth of the node represented by the function call of the traversal.)

5. Using an array of counters, tabulate (record) the number of nodes at each depth. (If int A[50] is the array of counters, and a node has depth d, then do (A[d])++.) You should also tabulate the number of leaf nodes at each depth.

6. Below I show the results of using the given 10 "random" numbers in the array R.

   Random Nos R[0]=0.56 R[1]=0.12 R[2]=0.93 R[3]=0.53 R[4]=0.74 R[5]=0.66 R[6]=0.89 R[7]=0.05 R[8]=0.76 R[9]=0.35 Leaf Node Counts Counts L[0]=0, A[0]=1 L[1]=0, A[1]=2 L[2]=1, A[2]=3 L[3]=2, A[3]=3 L[4]=1, A[4]=1 L[5]=0, A[5]=0 L[6]=0, A[6]=0 L[7]=0, A[7]=0

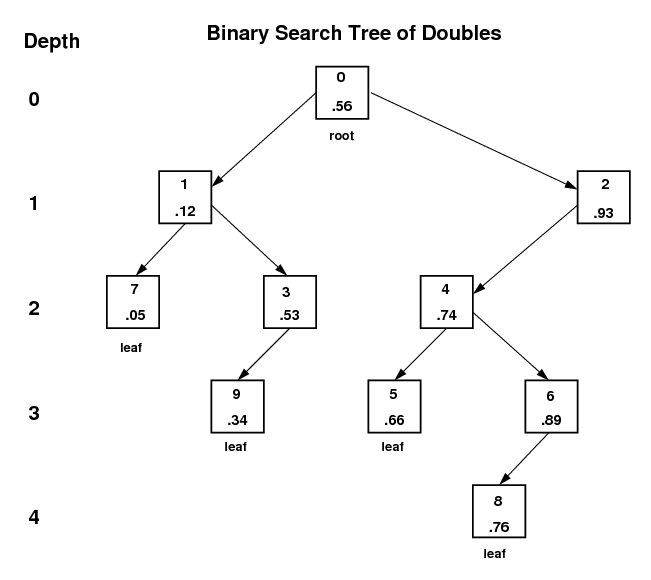   Click picture or here for full size picture.

   The depth of this tree is of course the largest index of a non-zero entry, using either the count of all nodes or of all leaf nodes. (Once an index i has A[i] = 0, we know that all entries are zero for any index j > i.) You must use this example to test your program initially, showing the results of a run. (Just patch in a curly bracket {} initialization of the array.)

7. Carry out the experiment for as large a number of doubles as your computer can handle (within reason -- I was able to use n = 10000000.) Then compare your maximum depth with 3 * log₂(n).

   [Here is my experiment: Depth of Random Binary Search Trees. All my experiments had maximum depth come in less than the book's upper bound for the expected height. Of course the actual height of a "randomly built binary search tree on n distinct keys" could be n, but this outcome has vanishingly small probability for large n.] keys