(Textbook. Click for information.)

CS 3343/3341  Analysis of Algorithms  Spring 2012  Recitation 13  Final Exam Review     Partial Answers

See Online Materials for links to topics covered in the course.

Topics NOT COVERED on the Final Exam. Each of these was covered earlier.

• Weird topics numbered 1,2,3,4,5, and 8 inclusive.
• Induction proofs.
• Proofs of correctness of algorithms using loop invariants.
• Solving recurrences with the Master Theorem and with recursion trees.
• The slow and quick exponentiation algorithms.
• Finding the median with a variation of quicksort.
• No heaps, heapsort, priority queues based on heaps (but you need to know what a priority queue is).

---

1. Quicksort and Randomization:
   1. Give the algorithm that randomizes the order of the elements in an array. What is it's asymptotic (time) performance? This elegant algorithm is half-way through the material on the page Randomize an Array.
   2. What is the worst-case asymptotic (time) performance of quicksort? O(n²)
   3. Explain how you could use Part i above to improve the performance of quicksort. Randomize the array to be sorted using part i before invoking quicksort. What kind of time performance does this give? Average-case time performance of O(n*log(n)). The worst-case performance is still O(n²) What "awkward" input case(s) does this help with? For your text's initial quicksort algorithm, one example is an array already in sorted order. Reverse sorted order is another example. Does this step eliminate these cases altogether? No, because for example, it is possible that the randomization would yield sorted order. If not, then why and how does this step help? For large n this is of vanishing small probability.
   4. Explain how the same technique would eliminate some of the same "awkward" input cases if one used a binary search tree for sorting. Randomizing the order before inserting into a binary search tree yields on average a depth (or height) bounded by 2*n*log(n). Searching would be efficient in such a tree: O(n*log(n)). Also: how would you use a binary search tree for sorting? Insert the array to be sorted into the binary search tree. Then output with an inorder traversal. What kind of performance does this "tree sort" algorithm have?
   5. Your text's Randomized Quicksort is different from Parts i and iii above. Explain the additions to the quicksort algorithm that give Randomized Quicksort. In the step of quicksort that partitions from index p to index r, generate a random integer i from p to r inclusive. Exchange the pivot in position A[r] with the element in A[i]. Then do the regular partition.

   ---

2. Dynamic Programming: Not sure if I'll have a problem on this.

   ---

3. Breadth-First and Depth-First Searchs of Graphs: By hand, run through a BFS and a DFS for the graph below, starting with vertex a. Assume that vertices are ordered alphabetically in the adjacency lists. Show the vertices in the order that they are visited. Use a queue (of coures) for BFS and a stack for DFS. (A stack for DFS gives the same order of visits, but not the same finishing times as recursion. I don't care about this here because I'm just asking for the order of the visits. Notice that as you process vertex a in DFS, you will push b and c in that order, so that c will be popped and will be the next vertex processed.) [It is important for you to do this by hand, rather than using your program, as practice for the final. This problem came from C. Wenk.]
   

   [Answers: For BFS, the order of vertices visited is: a,b,d,c,e,f. For DFS, the order of vertices visited is: a,d,e,f,c,b.]

   Queue: add at right, remove from left BFS Queue Action Add to Queue a Remove a and visit a Add b, d b d Remove b and visit b Add - d Remove d and visit d Add c, e c e Remove c and visit c Add f e f Remove e and visit e Add - f Remove f and visit f Add -

   Stack: push at right, remove from right DFS Stact Action Push on Stack a Pop a and visit a Push b, d b d Pop d and visit d Push c, e b c e Pop e and visit e Push f b c f Pop f and visit f Push - b c Pop c and visit c Push - b Pop b and visit b Push -

   ---

4. Graph Representations: Draw the adjaceny list representation for the directed graph in the previous problem. [Annoying to put into text, but this is practice for the final, where it will easy to draw it.]

   ---

5. Dijkstra's Algorithm: By hand, run through Dijkstra's algorithm on the graph below, starting with vertex a. Assume each undirected edge is two directed edges with the same weight in each direction. [As usual, this is awkward to put into text form, but for each stage you can give a line with the vertices still in the priority queue, and the current distance values to each vertex. It is important for you to do this by hand, rather than using your program, as practice for the final. This problem came from C. Wenk.]

   A star (*) marks those vertices that have been removed from the priority queue and processed (visited).

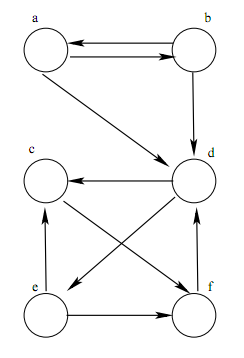
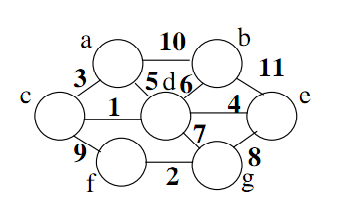
   Action	Contents of Piority Queue (* = removed)
   Remove & Relax	a	b	c	d	e	f	g
   Initial	0	∞	∞	∞	∞	∞	∞
   a	0*	10	3	5	∞	∞	∞
   c	0*	10	3*	4	∞	12	∞
   d	0*	10	3*	4*	8	12	11
   e	0*	10	3*	4*	8*	12	11
   b	0*	10*	3*	4*	8*	12	11
   g	0*	10*	3*	4*	8*	12	11*
   f	0*	10*	3*	4*	8*	12*	11*

   ---

6. Hashing: You had several problems about hashing in Recitation 12. [There will be a question about hashing on the final. See hashing and answers to Recitation 12.]

   ---

7. Reductions Involving Arithmetic Problems: Recall that we looked at 4 problems:
   P_m = multiplication of two numbers (a* b)
   P_d = division of two numbers (a/b)
   P_r = reciprocal of a number (1/a)
   P_s = square of a number (a²)
   

   We also used the relation ≤ to mean "efficient reduction".

   1. Of the two relations, P_m ≤ P_s and P_s ≤ P_m, one of them is trivial, and one depends on the formula:
      

      Which is which? For the relation that is trivial, why do I call it "trivial"? And for the relation that depends on the formula, explain (briefly) how the formula shows that the relation holds. The second one P_s ≤ P_m is trivial because multiplication includes squaring as a special case. If you can multiply, then certainly you can square. For the other direction P_m ≤ P_s, this asks to reduce multiplication to squaring, that is, if you can square (and can add, subtract, and multiply/divide by powers of 2), can you multiply? The formula make this obvious: how you can substitute 2 or 3 squares for one multiply.

   2. Use the formula below and the previous one to argue that: P_m ≤ P_r. First it is again almost obvious that P_s ≤ P_r: if you can take reciprocals, then by the formula, with 3 reciprocals (plus 2 subtractions and 1 addition, you can square. Next, since we know from part i that P_m ≤ P_s, then transitifity gives P_m ≤ P_r. (We didn't prove transitifity for this relation, but it's true.)
      

   ---

8. Hamiltonian Cycles:
   1. Give the definition of the Hamiltonian Cycle Problem (HP). (We also called it the Hamiltonian Circuit Problem.)
   2. Does the graph of state capitals have a Hamiltonian Cycle? (Careful here.) No, but it has a Hamiltonian Path.
   3. Does a complete graph always have a Hamiltonian cycle? Yes, obviously, since you can proceed from any vertex to any other on an edge (complete=all edges exist).
   4. One of the weird topics (but not Topic 10) talked about proving something involving a Hamiltonian Cycle. What was it?
   5. State the Traveling Salesman Problem (TS).
   6. We proved something involving HC and TS. What was it?
   7. State the Vertex-Cover Problem (VC).
   8. We talked a little about the proof that VC ≤_p HC. First of all, what does this formula say about VC and HC? Very roughly (without any details), what must one prove to prove this relation?

   ---

9. Two NP-complete Problems: Subset-Sum and Partition: We already looked at the Subset-Sum Problem (Recitation 7), but the notation below is slightly different than before:

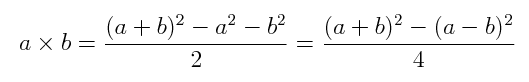
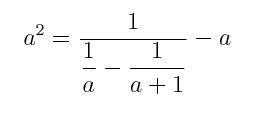
   Subset-Sum Problem (SS): Start with a set A of positive integers and a desired sum S. The decision question: Is there a subset A' of A such that sum( a | a in A' ) = S?

   Next is the Parition Problem (PART):

   Partition Problem (PART): Start with a set A of positive integers. The decision question: Is there a subset A' of A such that sum( a | a in A' ) =  sum( a | a in A - A' )? [Here A - A' is the complement of A' in A.]

   Show that PART ≤_p SS, that is, show that PART can be reduced to SS.

   [Hints: You need to start with an arbitrary problem in PART. Then come up with a way to transform any problem P in PART into a problem P' in SS. Finally show that the answer is "Yes" to P if and only if (exactly when) the answer is "Yes" to P'.]

   As in the hint, start with an instance P of PART, that is, start with an array A of positive integers. We assume that we can solve the SS problem. In order to answer "Yes" to P, we need to find a subset A' of A such that sum( a | a in A' ) =  sum( a | a in A - A' ).

   So construct an instance P' of SS. The array A in SS will be the same as the one in PART. Let T be the sum of all elements of A: T = sum( a | a in A ). If T is odd, then the answer to P' is immediately "No". Otherwise, use SS to try to find a subset A' such that S = T/2 = sum( a | a in A' ). Then clearly S = T/2 = sum( a | a in A-A' ). There will be such a subset A' given by SS iff and only if the same subset A' works to solve P in PART.

   ---

10. Turing Machines, Undecidable Problems: Consider the following "mystery" program in the language used for our Turing machines:

    Instructions in the Turing Language Instruction Representation Op Code print 0 000 0 print 1 001 1 move left 010 2 move right 011 3 stop 100 4 if 0 is scanned  goto i 101 0...0 1     <-i-> 5 if 1 is scanned  goto j 110 1...1 0     <-j-> 6 (end marker) 111 -

    Mystery Program ?? Instruction Representation 1. move left 2. if 1 is scanned goto 1 3. if 0 is scanned goto 4 4. print 1 5. move right 6. if 1 is scanned goto 5 7. print 1 8. move right 9. if 0 is scanned goto 1 10. stop (end) Initial ...0000000000... tape: | 010 110 1 0 101 0000 1 001 011 110 11111 0 001 011 101 0 1 100 111

    1. Explain carefully what this mystery program does. What is its output and what actions does it go through to produce this output? (This is easier than you might think, although in a sense it's a bit of a trick.) This is a TM that will never halt. It keeps going back and forth, tacking a "1" on at either end of a ever-growing sequence of 1's. In more detail:

       lines 2-3 search left for the first 0.
       line 4 overwrites this first 0 with a 1.
       lines 5-6 search right for the first 0.
       line 7 overwrites this first 0 with a 1.
       line 8 moves one more square right, where we know there is a 0.
       line 9 always goes back to step 1, since we know the current square is 0.
       line 10 is never executed.

       The execution will never stop; it goes on indefinitely (or "forever"). But there will never be more than finitely many 1s on the tape.

    2. Three of the instructions in this program can be replaced by a single instruction in such a way that the resulting program still prints 1's on the tape in the same places and in the same order. Can you figure out which 3 instructions could be replaced by one instruction? (Also a bit of a trick.) From the above, lines 8, 9, and 10 could be replaced by
       line 8: if 1 is scanned goto 1.
       Since line 7 wrote a 1, line 8 will always transfer to step 1. There is no need for a stop instructon at line 9, since it would never be executed.

       Note: It would be difficult to produce a simple program that started with a blank tape, did something non-trivial, and then halted. Part of the trouble is that the program could only generate a constant like 10 with 20 instructions. The only simple programs I could think of had infinite loops, so I decided to go for it.

    ---

11. All "sufficiently powerful" models of computation known up to now have equivalent computing power. These are called Turing Complete. They include all the normal programming languages and all the usual computers. The Church-Turing Thesis is the axiom (or hypothesis) that no more powerful model can exist. But common models are not Turing complete. Take for example the Finite Automata (FA) (aka Finite-State Machines). The rule is: "FAs can't count." A given FA isn't even powerful enough to count to an arbitrary number. An FA equiped with a stack (called a "Push-down Automaton) can count, but it still isn't complete.

    Usually we want our programming languages to have lots of nice and powerful instructions so that they are easy to program -- so that we can write short but powerful programs. OK, finally here is the question: Why did Turing make his machine as simple as possible? Why are the other Turing machines also simple like this and almost impossible to program? What's the advantage of being so simple? The huge advantage of simple models for TMs is that we can simulate the TM more easily in another environment. So simulate a TM inside the game of Life, and you can prove that some questions about Life are undecidable. From being able to simulate a TM within Life, we know that we could simulate any actual piece of hardware or software within Life, but the details are daunting. (As I said, crazy people have created more traditional machines within Life.)

    We would never want to use a Turing machine to do any actual computations. This is similar to not wanting (normally) to use machine language. If you had to write a bunch of machine language, unless you were crazy, you would write your own simple assembler, or at least a macro processor, or both.

    ---

12. Write a short essay on the theological implications of the Game of Life. Just kidding, although some of these issues are explored in many places on the net, for example, Simulated Evolution.