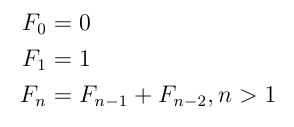Introduction to the Design and Analysis of Algorithms
Textbook.
 CS 3343/3341
 Analysis of Algorithms
 Fall 2012
 Recitation 5
 Newton's Method, Exp, etc. 
    Partial Answers  

  1. The first problem will be made accessible during the Recitation hour: Rec 5, In-Class Problem 1 (password protected, use "CS3343" without quotes for "User Name" and password from class just before the recitation). [The following page includes a discussion that answers all parts of this question: division using Newton's Method.]

  1. Consider Problem 1 of Recitation 4, the in-class work on an algorithm to find the median of n numbers in an array in average-case time of O(n). Assume that the algorithm proceeds with a more-or-less equal-sized split each time a partition is done. (Each time a partition is done, the pivot ends up roughly in the middle.) Use the recursion tree approach to analyze the big-O performance of the median algorithm under this assumption. [The tree you are to create will resemble the tree in the first image of the link above. Of course you need to conclude that the algorithm will be O(n).]

    [Here is a recursion tree similar to the one for quicksort at the link above, except that there is only one branch downward at each stage.]

      ^        c * n     ------->  c * n
  |          |
  |          |
  |       c * n/2    -------> c * n/2
  |          |
  |          |
  |       c * n/4    -------> c * n/4
  |          |
log2(n)      |
  |       c * n/8    -------> c * n/8
  |          |
  |          |
  |         ...         ...
  | 
  |          |
  v          c       -------> c 

                             ________

Total: c*n + c*n/2 + c*n/4 + c*n/8 + .. c

  <= c*n(1 + 1/2 + 1/4 + 1/8 + ...) 

     = c*n*2 = Θ(n)

  1. Recall the Fibonacci Numbers: F0 = 0, F1 = 1, F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, F7 = 13, F8 = 21, F9 = 34, F10 = 55, ... . These are defined recursively by:

    There are infinitely many formulas involving Fibonacci numbers. Here's a hint for you to discover one of these: Let Sn denote the sum of Fi for i from 0 to n. Write down the values of the first 10 or so of the Sn. They start out this way: 0, 1, 2, 4, 7, .... Now you should be able to guess a formula for Sn. (If nothing hits you over the head, check your arithmetic and write down some more of them.) Use induction to prove that this formula is correct. [Just one more try at induction: First establish the base case: in this example show that your formula is true for n = 0. Next assume that your formula is true for n. Use that assumption to prove the formula is true for n+1.] [Well, there are at least two "obvious" formulas:

    [A variation on the first formula is:

    Let's prove them both by induction. In each case, the basis (n = 0, 1, 2) is obvious. First formula:

    Second formula:

    It is also easy to see without induction that each formula implies the other.]

Revision date: 2012-09-22. (Please use ISO 8601, the International Standard.)