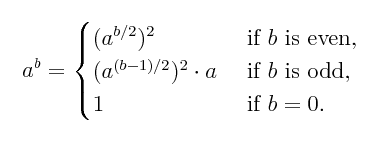CS 3343/3341: Recitation 4 Answers, Quicksort, Exp, etc.

Introduction
to the Design and Analysis of Algorithms

Textbook.

CS 3343/3341
Analysis of Algorithms
Fall 2012
Recitation 4
Quicksort, Exp, etc.
Partial Answers

The first problem will be made accessible during the Recitation hour: Rec 4, In-Class Problem 1 (password protected, use "CS3343" without quotes for "User Name" and password from class just before the recitation). [Answers are at: answers]

The pow(x, y) function calculates x^y. Implement pow using just the log and exp functions in Java or C. [Both these functions are base e. The logs page would be helpful. The answer is directly given in Java on this page. ]

The three versions of exponentiations are explored in exponential algorithms:

Consider the "Modular-Exponentiation" algorithm in your textbook page 957, shown in the image below. The algorithm has several features not relevant to this discussion: Since it is a part of the RSA cryptosystem implementation, there is an extra parameter n, and at each stage, the algorithm takes the remainder on division by n. The variable c is used only for a proof of correctness. Eliminating n and c, and changing it to the C language, we get the function on the left below. The original algorithm from class is given at the right below.

// expon: calculates a^b, where // b = b[k] b[k-1] ... b[0] (binary) // Rewritten from your text. int expon(int a, int b[], int k) { int d = 1; // final result int i; for (i = k; i >= 0; i--) { d = d * d; if (b[i] == 1) d = d * a; } return d; }

// expon: fast exponentiation // presented in class int expon(int a, int b) { int d = 1; // final result while(b > 0) { if (b%2 == 1) d = d*a; b = b/2; if (b > 0) a = a*a; } return d; }

Convince yourself that these algorithms are different by tracing through the execution of each one, using the inputs a = 3, and b = 22 = 10110₂. [Be sure to keep the two separate. For each loop execution, show the results of the two assignments (one only conditionally executed). Be careful, because b on the left is an array, but an int on the right. If you like, you can show the results as powers of 3. The final answer in each case is 3²² = 31 381 059 609.] [The most important difference between the book's algorithm (at the top and left above) and the algorithm given in class (at the right above) is that the former processes the bits of the exponent from right to left (most sig to least), while the class algorithm processes the bits of the exponent from left to right (least sig to most).]

The following is a recursive definition of a^b for integers a and a. (This example is due to A. Levitin, from his algorithms text.)
1. Implement this definition in Java or C using recursion. [Just follow the definition. I used an extra function int sqr(int r){ return r*r; }, since Java and C don't have a squaring or exponentiation operator. (Why not? Couldn't they use ^ for this, or ** like Fortran?).] [This implementation is also at the earlier link above. As for the other "frivolous" question, ^ is already an operator in C and Java (XOR). ** would be crazy to try to use, since C and Java already make extensive use of *. Also exponentiation has often depended on the particular numerical library used.]
2. Use your program to calculate 3¹⁹ and 5¹³.
3. This program does essentially the same calculations as one of the two earlier methods above. Which one do you think? [Don't just guess or spend a lot of time on this.] [During the process of the recursive calculation, the exponent b in a^b is successively replaced by b/2 or by (b-1)/2 depending on whether b is even or odd. This continues by recursive calls until b is 0. Only then does the algorithm begin to carry out computations, first returning 1. The computations occur in the reverse order to the way the b values were first generated. The b values were generated from least significant to most significant, so the computations will occur from most significant bit of the exponent down to least significant, and this is the order used in the algorithm from the text, the one that uses the explicit binary version of the exponent. (This text's algorithm starts with 1, and either squares what is to be returned or or multiplies by a, just at the recursive algorithm does.)]

This problem deals with the Fake Coin Weird Topic.
1. What about n not an exact power of 3? Say in detail how you would handle this. [Take three piles: P, Q, and R, where P and Q have the same number of coins. The system still works fine, but it will finish the quickest if the three are as near in size as possible. Suppose P and Q have n coins and R has n, or n+1, or n+2. You weigh P and Q. If they balance, R has the coin. Otherwise the lighter of P and Q has the coin. This will still take roughly log₃(n) + 1 steps.]
2. We improved from log₂(n) steps to log₃(n). By what factor did the number of steps improve?
  c = log₃(n) / log₂(n), and
  log₃(n) = log₂(n) / log₂(3), so
  c = 1 / log₂(3) = 1 / 1.58496 25007 = 0.63092 97535
3. Suppose we don't know whether the fake coin is heavier or lighter. Can you handle this case efficiently? (One or a few extra weighings.) (And, hey, not just a "Yes" or "No" answer!) [This can be done almost as in part ( i ), but with at most 1 extra weighing. Start with piles P, Q, and R as before. Again suppose P and Q have n coins and R has n, or n+1, or n+2.
  Weigh P and Q.
  1. If they balance, R has the coin (could still be lighter or heavier).
  2. If P is heavier, weigh P and R (with 0, 1, or 2 coins missing, to make it the same size as P and Q).
  2a. If P and R balance, Q has the lighter coin.
  2b. If P is still heavier, P has the heavier coin.
  3. If P is lighter, weigh P and R (with 0, 1, or 2 coins missing, to make it the same size as P and Q).
  3a. If P and R balance, Q has the heavier coin.
  3b. If P is still lighter, P has the lighter coin.
  At the end of the above process, you are left with a new pile in which one has:
  1. Done one weighing, and reduced the size of the pile holding the coin by roughly 1/3. The coin could still be lighter or heavier.
  2. Done two weighings, reduced the size of the pile holding the coin by roughly 1/3, and determined whether the coin is heavier or lighter. In this case one can proceed as in question ( i ) above.
  The whole process can be repeated as long as the size of the remaining pile is >= 3. If the pile is down to size 2, then 1 weighing will suffice if you know whether the fake coin is lighter or heavier. Otherwise 2 weighings are needed.
  If the pile is down to size 1, then you are done if you know whether the fake coin is lighter or heavier. Otherwise 2 weighings are needed.
  We only need the extra weighing one time when we determine whether the coin is heavier or lighter (but we don't know when this will be determined).]

Revision date: 2012-10-04. (Please use ISO 8601, the International Standard.)